Теорема Ферма

И.И. Лещенко

Последняя теорема Ферма. Наглядное изображение.

Москва 2013 г.

1. Введение

Цель работы – представить Последнюю теорему Ферма в наглядном виде. Графические схемы обеспечивают новые возможности, – если не для доказательства теоремы, то, во всяком случае, – для выяснения причин, способствующих целочисленному решению радикала ⁿv[xⁿ+(x+С)ⁿ] при n=2 и исключающих его при n?2 (С – целое число, равное разнице y и x в уравнении Ферма).

Главными графическими элементами однотипных – для каждого показателя степени – схем служат кривая и множество точек. Формула кривой и координаты точек сконструированы таким образом (см. раздел 2), что совместимость двух названных элементов графика свидетельствует о целочисленном решении радикала, несовместимость – о дробном иррациональном результате.

Все абсциссы кривой (абсциссы вершин тупых углов ломаной линии, условно именуемой кривой) и точек – целые числа, ординаты – иррациональные бесконечные десятичные дроби. Бесконечность двух иррациональных ординат – кривой и точек, – рассчитываемых по разным формулам, почти всегда предопределяет обоюдную несоизмеримость. Для их равенства, для совместимости кривой и точек на графике необходимы особые – идеальные условия. Они обеспечиваются только в рамках графической схемы второй степени, анализ которой играет ключевую роль в понимании (решении) проблемы, поставленной теоремой Ферма.

Чтобы понять, почему невозможно целочисленное решение радикала при n?2, необходимо, как минимум знать, почему оно возможно при n=2, в чём первопричина образования пифагоровых троек. Теорема Пифагора лишь фиксирует соотношение сторон прямоугольного треугольника, не объясняя его частных случаев: независимо от значений длины катетов – целочисленных, рациональных или иррациональных, – сумма их квадратов равна квадрату гипотенузы; но не во всех случаях, даже при целочисленных катетах, то же – целочисленное – значение принимает гипотенуза. В предлагаемой работе каждый случай получает своё объяснение; кроме того, в прил.4-6 показано, что пифагоровы тройки – лишь частный случай более общей закономерности.

Несмотря на оговорки в различных формулировках теоремы Ферма, ограничивающие внимание ко второй степени, в предлагаемой работе, наоборот, уникальным особенностям её графической схемы отводится решающая, ключевая роль. На их систематизации, включая классификацию пифагоровых троек (прил.4-7), и сравнительном анализе базируется логика выяснения причин совместимости/несовместимости кривой и точек и, соответственно, – целочисленного и рационального или иррационального значения длины гипотенузы прямоугольного треугольника.

Одна группа особенностей схемы второй степени требует доказательства своей уникальности: в первую очередь, – собственно теорема Ферма и её графический аналог – совместимость точек и кривой. Особенности другой группы в наглядном изображении – при сравнении графических схем с n=2 и n?2 – вполне очевидны даже на небольших отрезках бесконечного графика, и доказательства их уникальности не требуется. Достаточно очевидны и причинно-следственные связи между двумя группами уникальных особенностей. Задача работы – показать подобные связи, что облегчит общее доказательство теоремы, или сделает его необязательным, заменив наглядным объяснением.

Работа состоит из описательной и конструктивной части. В первой (разделы 2-3) – приведена характеристика основных параметров графической схемы, включая обоснование зоны начальной несовместимости (ЗНН) точек и кривой, и характеристику ограничивающей ЗНН критической точки. Во второй части (раздел 4) рассмотрены уникальные особенности графической схемы второй степени и схема доказательства несовместимости критической точки (и других точек) и кривой – при n?2.

Для наглядного изображения теоремы Ферма предложена новая, ранее не использовавшаяся графическая схема. В связи с этим она представлена в работе более детально, чем требуется для решения поставленных задач. Имеются ещё более детальные варианты настоящей работы, пока не опубликованные, но получившие авторские свидетельства.

Работу не следует определять как математическую. Скорее, это попытка решения головоломки с применением азов математического анализа и аналитической геометрии.

Вместе с тем, работа по существу представляет собой схему, которая – при её одобрении – могла бы развиваться и совершенствоваться профессиональными математиками.

2. Общая характеристика графических схем

Каждая из однотипных графических схем (для каждого показателя степени n) состоит из кривой (2-1)¹⁾ и множества точек с абсциссами х и ординатами, определяемыми по (2-2)¹⁾.

О_КРВ=C+х*(ⁿv2)–ⁿv[хⁿ+(х+C)ⁿ], (2-1)

где О_КРВ – ордината кривой.

С – целое число, равное разнице y и x в уравнении Ферма – xⁿ+yⁿ=zⁿ (C=y–x); далее для простоты принято С=1 (в самом последнем прил.4-7¹⁾ обоснована возможность распространить полученные при С=1 выводы на все целые значения параметра).

х – абсциссы рядовых (и других) точек – числа их натурального ряда, включая ноль.

Ординаты точек (О) – иррациональные бесконечные десятичные дроби:

О=х*(ⁿv2)–целая часть десятичного числа (ЦЧДЧ) (2-2)¹⁾

При выбранном способе построения вертикальное расстояние между кривой и ближайшей точкой равно разности ⁿv[xⁿ+(х+1)ⁿ]–ближайшее целое число (БЦ). Если разность положительна, точка расположена выше кривой, если отрицательна – ниже, если разность равна нулю (иногда – при n=2), точка лежит на кривой, и из-под корня извлекается целое число. Таким образом, формула кривой позволяет сформулировать наглядный признак целочисленного решения радикала ⁿv[xⁿ+(х+1)ⁿ]: если оно существует, два из трёх членов правой части (2-1) – целые числа, и дробные части ординаты кривой и произведений х*(ⁿv2) должны совпадать. Именно из-за интереса к дробной части целая часть исключается при расчёте ординат точек по (2-2).

В соответствии с признаком целочисленного решения радикала ⁿv[xⁿ+(х+1)ⁿ], доказательство теоремы сводится к доказательству несовместимости точек и кривой.

Подстановкой больших значений х в общий член ряда радикалов устанавливается, что:

lim_x>?{ⁿv[xⁿ+(x+1)ⁿ] / ⁿv2} = x+0,5

и lim_x>?{ⁿv[xⁿ+(x+1)ⁿ]} = (x+0,5)*ⁿv2 (2-3)

Последующей подстановкой (2-3) в (2-1) определяется предел кривой:

lim _x>?О_КРВ = lim _x>?{1+х*(ⁿv2)–ⁿv[хⁿ+(х+1)ⁿ]} = 1+х*(ⁿv2)–(x+0,5)*ⁿv2 =

= 1+х*(ⁿv2)–х*(ⁿv2)–0,5*(ⁿv2) = 1–0,5*(ⁿv2) =

= 1–0,5*(ⁿv2)+0,5–0,5 = 0,5–0,5*[(ⁿv2)–1] (2-4)

При n>? пределы кривых имеют собственный предел (2-5): поскольку lim_n>?(ⁿv2)=1, то

lim х>? (lim х>? О_КРВ) = 0,5–0,5*(1–1)=0,5 (2-5)

Рядовые точки образуют бесконечное множество систем параллельных линий. На графиках (рис.2-1)¹⁾ прослеживаются только первые из них – с наиболее крутыми линиями. Большинство систем с пологими линиями не видны из-за больших расстояний между точками по горизонтали и ограниченной – реальной – длины графика.

У каждой системы – индивидуальные параметры: угловые коэффициенты прямых линий и соответствующие им приращения абсцисс и ординат. Системам с восходящими линиями соответствуют положительные приращения ординат и нечётные порядковые номера, системам с нисходящими линиями – отрицательные приращения и чётные номера (табл.2-1)¹⁾. Приращения абсцисс и абсциссы точек – положительные целые числа. Рядовыми приращениями ординат (П_О) и абсцисс (П_А) названы, соответственно, вертикальные и горизонтальные проекции отрезков прямых линий между соседними точками.

Словосочетания «приращения ординат» и «приращения абсцисс» относятся только к разнице координат точек. «Прирост ординаты кривой» каждый раз в дальнейшем оговаривается специально и определяется в расчёте на единицу значения аргумента – абсциссы х.

Каждая система параллельных линий включает первую прямую. Первая восходящая прямая (по отношению к кривой – нулевая хорда) начинается в начале координат, нисходящая – в точке с координатами (0; 1). Первые точки на первых прямых названы направляющими (рис.2-1, 2-2); их координаты определяют стандартные для каждого показателя степени приращения абсцисс и ординат (П_А/i; П_О/i). Последние, в свою очередь, определяют угловые коэффициенты параллельных линий каждой системы: tg?_i=П_О/i/П_А/i. Все направляющие точки входят в подмножество точек, ближайших к горизонтальным ограничениям элементарного графика; их ординаты могут рассчитываться как по (2-2), так и по формулам графы 2 табл.2-1.

---

¹⁾Первая цифра в скобках – номер раздела, вторая – номер формулы, рисунка, таблицы или приложения.

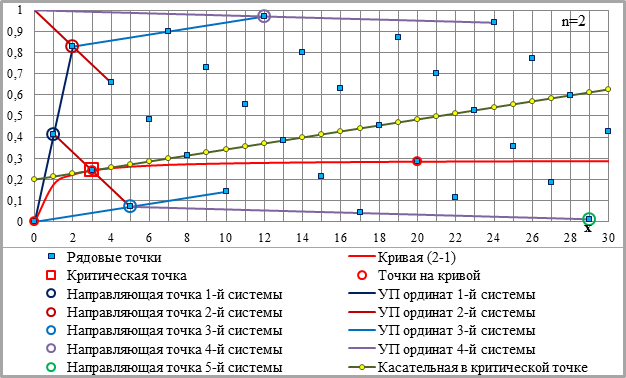
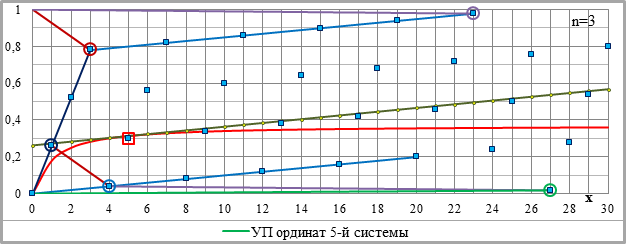
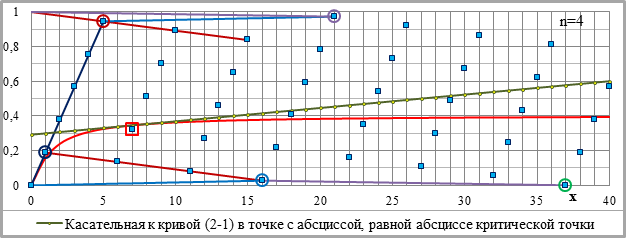
Рис.2-1. Основные параметры графической схемы – кривая (2-1), критическая точка, рядовые и направляющие точки и укрупнённые приращения ординат (УП_О). Сверху вниз: n=2, n=3 и n=4; С=1. Легенда – на всех графиках, фрагменты графиков – см. рис.2-2 на следующей странице.

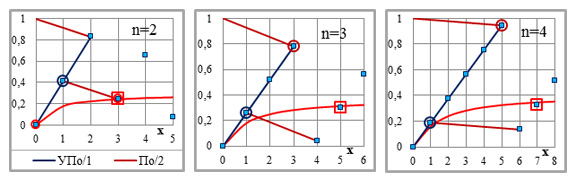
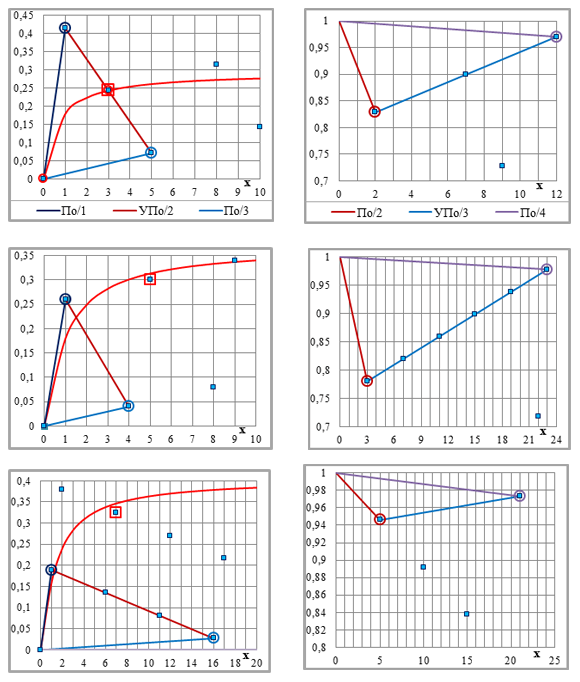
Рис.2-2. Фрагменты рис.2-1 с расчётами приращений ординат (внизу). Рядовые и укрупнённые приращения ординат – П_О/i и УП_О/i=УК_i*П_О/i, i – порядковый номер системы параллельных линий. Показатели степени – на графиках; С=1 (легенда – на рис.2-1; на рис.2-2 – для трёх верхних графиков – на левом графике, для трёх пар графиков ниже – на верхней паре).

П_О/2=1–УК₁*П_О/1 (три графика вверху)

n=2 1–2*0,414214=0,171573 УК₁=1/0,414214–0,414214=2

n=3 1–3*0,259921=0,220237 УК₁=1/0,259921–0,847322=3

n=4 1–5*0,189207=0,053964 УК₁=1/0,189207–0,285214=5

П_О/3=П_О/1–УК₂*П_О/2 (графики слева) и П_О/4=П_О/2–УК₃*П_О/3 (графики справа)

n=2 0,071068=0,414214–2*0,171573 и 0,029437=0,171573–2*0,071068

n=3 0,039684=0,259921–1*0,220237 и 0,021816=0,220237–5*0,039684

n=4 0,027314=0,189207–3*0,053964 и 0,026651=0,053964–1*0,027314

Таблица 2-1

Схема расчёта приращений ординат, абсцисс (П_О и П_А) и укрупняющих коэффициентов (УК)

i	Рядовые приращения ординат (ПО/1, 2, 3 …) 1)	Укрупняющие коэффициенты (УК – всегда положительны)	Рядовые приращения абсцисс (ПА/1, 2, 3…) 1)
1	2	3	4
1	ПО/0= –1		ПА/0=0
	ПО/1=(nv2)–1		ПА/1=1
2		УК1=1/[(nv2)–1]–ДЧ12)
	ПО/2= 1–ПО/1*УК1		ПА/2=ПА/0+ПА/1*УК1
3		УК2=ПО/1/ПО/2–ДЧ2
	ПО/3=ПО/1–ПО/2*УК2		ПА/3=ПА/1+ПА/2*УК2
4		УК3=ПО/2/ПО/3–ДЧ3
	ПО/4=ПО/2–ПО/3*УК3		ПА/4=ПА/2+ПА/3*УК3
5		УК4=ПО/3/ПО/4–ДЧ4
	ПО/5=ПО/3–ПО/4*УК4		ПА/5=ПА/3+ПА/4*УК4
6		УК5=ПО/4/ПО/5–ДЧ5
	ПО/6=ПО/4–ПО/5*УК5		ПА/6=ПА/4+ПА/5*УК5
7		УК6=ПО/5/ПО/6–ДЧ6
	ПО/7=ПО/5–ПО/6*УК6		ПА/7=ПА/5+ПА/6*УК6
i		УКi–1=ПО/i–2/ПО/i–1–ДЧi–1
	ПО/i=ПО/i–2–ПО/i–1*УКi–1		ПА/i=ПА/i–2+ПА/i–1*УКi–1

¹⁾ Цифровой индекс внизу, в знаменателе – порядковый номер системы параллельных линий.

²⁾ ДЧ – дробная часть десятичного числа ДЧ_i–1=П_О/i–2/П_О/i–1–УК_i–1 ( табл.2-1, графа 3, строка i).

Для расчёта рядовых приращения ординат (П_О/i) друг на друга делятся абсолютные значения двух предыдущих приращений (П_О/i–2 / П_О/i–1). В качестве исходного рядового отрицательного П_О/0 принята единица – высота элементарного графика при С=1, первое положительное приращение (П_О/1) по принятым условиям построения равно (ⁿv2)–1 (табл.2-1). Укрупняющим коэффициентом (УК) названа целая часть результата деления друг на друга двух предыдущих П_О. Произведение УК на рядовое приращение названо укрупнённым приращением (УП_О=П_О*УК), состоящим из одного или нескольких рядовых П_О. Разница, или алгебраическая сумма, рядового (П_О/i–2) и следующего по порядку УП ординат (УП_О/i–1) определяет следующее рядовое приращение (П_О/i) и т.д. (табл.2-1, рис.2-2 – подрисуночные расчёты).

Рядовые приращения абсцисс рассчитываются, как сумма их рядового приращения на линии, предшествующей предыдущей, и укрупнённого – на предыдущей линии:

П_А/i=П_А/i–2+П_А/i–1*УК_i–1 (табл.2-1, графа 4). Используя эту формулу, рядовые П_А (они же – абсциссы направляющих точек – х_НПР-i) можно представить в виде функций укрупняющих коэффициентов (2-6):

П_А/0=0; П_А/1=1; П_А/2=0+1*УК₁=УК₁

П_А/3=1+УК₁*УК₂ (2-6)

При известных приращениях абсцисс приращения ординат (они же – ординаты направляющих точек – O_НПР-i) могут определяться иным способом (2-7):

П_О=П_А*(ⁿv2)– БЦ, (2-7)

где БЦ – ближайшее к уменьшаемому произведению П_А*(ⁿv2) целое число.

Если П_А*(ⁿv2)>БЦ, приращение ординат – положительно, если П_А*(ⁿv2)<БЦ – отрицательно. Используя формулы (2-6) и (2-7), в виде функций УК можно представить рядовые П_О, например:

П_О/3=(1+УК₁*УК₂)*(ⁿv2)–БЦ (2-8)

Каждому показателю степени соответствует бесконечный график кривой с параметрами табл.2-1. Высокой степенью упорядоченности все параметры резко выделяются при n=2, – из-за постоянства отношений соседних приращений ординат.

Если принять П_О/1=[(v2)–1]=М, то

1/М=М/М²=М²/М³=М³/М⁴=… …=М^i–1/Мⁱ = М+2 = [(v2)–1]+2 = (v2)+1 = 2,4142, (2-9 а)

причём 1–2М=М², М–2М²=М³, М²–2М³=М⁴, М³–2М⁴=М⁵… …М^i–1–2Мⁱ=Мⁱ⁺¹ (2-9 б)

Таким образом, при n=2 все рядовые приращения ординат являются абсолютными значениями последовательно растущих степеней М (табл.2-2), а все укрупняющие коэффициенты равны двум.

Таблица 2-2

Растущие степени первого приращения ординат П_О/1 [(v2)–1]ⁱ=Mⁱ и суммы [(v2)+1]ⁱ при n=2

[(v2)–1]i=Mi	{хНПР*(v2)–БЦ1)} или {БЦ–хНПР*(v2)}	Значения
1	2	3=2
[(v2)–1]0	1	1
[(v2)–1]1	1(v2)–11)	0,414213562
[(v2)–1]2=[(v2)–1]*[(v2)–1]	2–(v2)–(v2)+1=3–2(v2)	–0,171572875
[(v2)–1]3=[3–2(v2)]*[(v2)–1]	3(v2)–4–3+2(v2)=5(v2)–7	0,071067812
[(v2)–1]4=[5(v2)–7]*[(v2)–1]	10–7(v2)–5(v2)+7=17–12(v2)	–0,029437251
[(v2)–1]5=[17–12(v2)]*[(v2)–1]	17(v2)–24–17+12(v2)=29(v2)–41	0,012193309
[(v2)–1]6=[29(v2)–41]*[(v2)–1]	58–29(v2)–41(v2)+41=99–70(v2)	–0,005050634
[(v2)+1]i	[хНПР*(v2)+БЦ]	Значения
[(v2)+1]0=	=1	=1
[(v2)+1]1=[(v2)+1]*1=	=1(v2)+11)=	=2,41421356
[(v2)+1]2=[(v2)+1]*[(v2)+1]=	=2+(v2)+(v2)+1=3+2(v2)=	=5,82842713
[(v2)+1]3=[2(v2)+3]*[(v2)+1]=	=4+3(v2)+2(v2)+3=5(v2)+7=	=14,0710678
[(v2)+1]4=[5(v2)+7]*[(v2)+1]=	=10+7(v2)+5(v2)+7=17+12(v2)=	=33,9705628
[(v2)+1]5=[12(v2)+17]*[(v2)+1]=	=24+17(v2)+12(v2)+17=29(v2)+41=	=82,0121933
[(v2)+1]6=[29(v2)+41]*[(v2)+1]=	=58+29(v2)+41(v2)+41=99+70(v2)=	=197,994949

¹⁾ БЦ – ближайшее к произведению х_НПР*(v2) целое число

Для соотношений соседних приращений абсцисс значение М+2 является пределом при бесконечном росте их порядковых номеров: lim_i>?(П_A/i–1/П_A/i)=М+2=(v2)+1=2,4142 (рис.2-3).

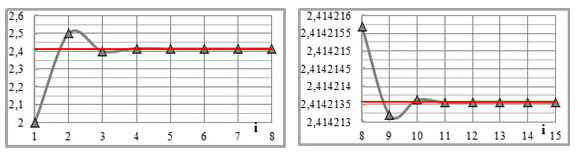
Рис.2-3. Соотношения соседних приращений абсцисс (П_А/i+1/П_А/i) при n=2.

Благодаря сплошной двоичности укрупняющих коэффициентов (только) в графической схеме при n=2 возникает два подмножества направляющих точек и, соответственно, два подмножества систем параллельных линий – основных и промежуточных или межсистемных (рис.2-4).

В каждом укрупнённом приращении координат (УП) при n=2 – два рядовых приращения и три ограничивающих их точки. На рис.2-5 крайние, ограничивающие УП, точки служат направляющими точками двух соседних чётных или соседних нечётных – систем параллельных линий, а точка в середине УП – межсистемной направляющей точкой с координатами (х_М/С; О_М/С).

Наличие двух подмножеств направляющих точек при n=2 отражается в генерации приращений ординат (П_О/i), каждое из которых, как отмечено выше, является последовательно растущей степенью П_О/1. Порядковый номер приращения i соответствует показателю степени; коэффициенты при радикале (v2) в двучлене, выделенные в графе 2 табл.2-2 жирным шрифтом, служат абсциссами основных направляющих точек (х_НПР), а ближайшие к произведению х_НПР*(v2) целые числа (БЦ) – абсциссами межсистемных направляющих точек (х_М/С).

Абсциссы основных направляющих точек последовательно совпадают с целыми числами а и b в формулах – a²–b², 2ab и a²+b² – для нахождения пифагоровых троек. Для этой цели можно использовать любую пару чисел, но пара абсцисс направляющих точек обеспечивает в получаемых тройках параметр С, равный единице (табл.2-3; прил.2-1). По существу направляющие точки самовоспроизводятся. Если с числами а и b последовательно совпадают абсциссы межсистемных направляющих точек, в получаемых тройках параметр С равен двум.

Совпадение при n=2 абсцисс направляющих точек с числами a и b в стандартных формулах, подчёркивает естественный характер предлагаемой графической схемы.

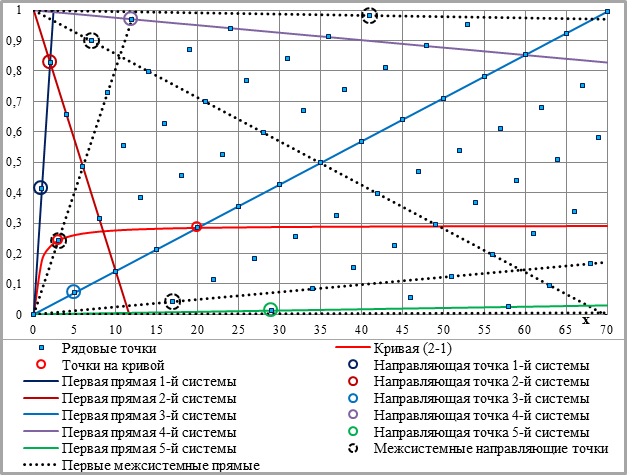
Рис.2-4. Основные и межсистемные направляющие точки и первые прямые (n=2, С=1).

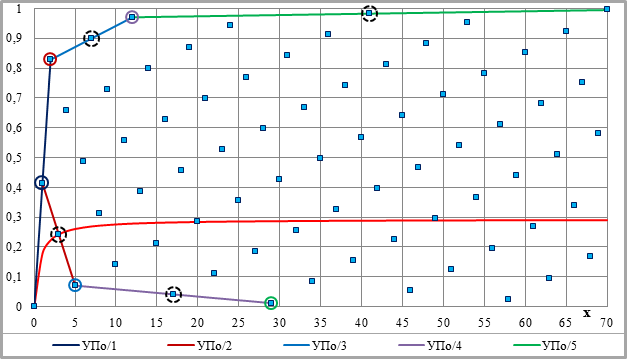
Рис.2-5. Укрупнённые приращения координат по системам параллельных линий – УП_А/i и УП_О/i (n=2, С=1). Легенда – на рис.2-4 и 2-5.

Таблица 2-3

Абсциссы направляющих точек – как числа a и b для нахождения пифагоровых троек (n=2, C=1); в графах 4 и 5 первые числа пифагоровых троек сдвинуты влево, вторые – вправо.

i	ai=ПА/i	bi=ПА/i +1 (все УК=2)	b2–a2	2ab	b2+a2
1	2	3	4	5	6
0	0	1	1	0	1
1	1	0+1*2=2	3	4	5
2	2	1+2*2=5	21	20	29
3	5	2+5*2=12	119	120	169
4	12	5+12*2=29	697	696	985
5	29	12+29*2=70	4059	4060	5741
6	70	29*70*2=169	23661	23660	33461
7	169	70+169*2=408	137903	137904	195025
8	408	169+408*2=985	803761	803760	1136689

При n>2 каждый из параметров табл.2-1 или их соотношения представлены на графиках с использованием в качестве независимого переменного показателя степени (рис.2-6, верхние графики; рис.2-7). Плоскостью подобных графиков служит вертикальная (фронтальная) проекция кривых.

С ростом показателя степени n рядовые приращения ординат уменьшаются, причём П_О/1 – плавно, равномерно (рис.2-6), все остальные – скачкообразно. С ростом n все укрупнённые приращения ординат скачкообразно уменьшаются, кроме УП_О/1, которое также скачкообразно растёт, стремясь к единице, или высоте элементарного графика. С ростом показателя степени УК₁ неограниченно растёт – из-за постоянной единицы в числителе уменьшаемого соответствующей формулы (табл.2-1, строчка 2, графа 3) и стремящегося к нулю его знаменателя; угловой коэффициент наклонной «прямой» графика УК₁ практически равен 1/ln2 (рис.2-7).

Рис.2-6. Верхняя пара графиков – динамика приращений ординат в зависимости от показателя степени; слева – рядовые (По), справа – укрупнённые (УПо). Нижняя пара графиков – динамика рядовых приращений ординат в зависимости от порядкового номера (i); легенда на левом графике.

Рис.2-7. Динамика первого укрупняющего коэффициента (УК₁).

В пределах каждого показателя степени с ростом порядкового номера (i>?) приращения ординат уменьшаются, причём при n=2 – равномерно, при всех n?2 – скачкообразно (рис.2-6).

Целочисленные приращения абсцисс с ростом показателя степени n и порядкового номера i увеличиваются, и только рядовые приращения абсцисс 1-й системы параллельных линий всегда равны единице: П_А/1=1 (табл.2-1, строчка 1, графа 4).

Чётные и нечётные значения УК₁ делятся поровну – по 50%; у всех прочих УК с большими порядковыми номерами преобладают (~2/3) нечётные значения (так как единица встречается чаще двойки, и далее – каждое предыдущее значение УК – чаще последующего).

Для УК₂ распределение долей получает строгое обоснование, благодаря упорядоченной динамике соотношений двух первых приращений ординат при росте показателя степени: чем больше УК₂, тем меньше его доля в общем количестве значений (2-10):

Д_УК-2=1/к–1/(к+1)=1/[к*(к+1)], (2-10)

где Д_УК-2 – доля УК₂ в общем количестве его значений графике П_О/2/П_О/1, к – значение УК₂.

Угловые коэффициенты (tg?_i) прямых i-той системы параллельных линий, соединяющих точки, рассчитываются делением приращения ординат на приращение абсцисс:

tg?_i = П_О/i/П_А/i = [П_А/i*(ⁿv2)–БЦ_i]/П_А/i = ⁿv2–БЦ_i/П_А/i, (2-11)

где БЦ – ближайшее к уменьшаемому произведению целое число [см. (2-7)].

Формулы угловых коэффициентов прямых различных систем параллельных линий (2-11) и касательных (2-12) к кривым, то есть производных (2-1), по своей структуре весьма схожи:

tg?_КСТ = {1+х(ⁿv2)–ⁿv[хⁿ+(х+1)ⁿ]}’ = ⁿv2–[х^n–1+(х+1)^n–1] / ⁿv[xⁿ+(х+1)ⁿ]^n–1, (2-12)

где tg?_КСТ – угловой коэффициент касательной.

У них одинаковое уменьшаемое – ⁿv2; вычитаемое представлено дробью, числитель которой в обоих случаях – натуральное целое число. Расхождение – в знаменателе вычитаемого.

Только когда точка с координатами [x; х*(ⁿv2)–целая часть десятичного числа] лежит на кривой, и её абсцисса обеспечивает целочисленное решение радикала ⁿv[xⁿ+(х+С)ⁿ], формула касательной (2-12) упрощается до tg?_КСТ=(ⁿv2)–рациональное число (2-11).

Горизонтальные расстояния между точками на прямых различных систем параллельных линий равны (или кратны) целочисленному знаменателю вычитаемого – П_А/i в (2-11). В полной мере это утверждение относится к касательным, – если точка касания лежит на кривой и сложный знаменатель (радикал) вычитаемого в (2-12) является целым числом [см. рис.2-1, где касательная с координатами точки касания (3; 0,2426) совпадает с прямой 3-й системы параллельных линий].

Вертикальное расстояние между любой точкой и прямыми линиями либо равно нулю, либо рациональной дроби, кратной 1/П_А/i.

Выводы, подчёркивающие разницу графических схем при n=2 и n?2:

1. При n=2 все укрупняющие коэффициенты (УК) равны двум, при n?2 это невозможно даже теоретически: УК₁ равен двум только один раз – при n=2, – далее, при n>? он только растёт.

2. Только в графической схеме второй степени насчитывается два подмножества направляющих точек и, соответственно, два подмножества систем параллельных линий – основных и промежуточных, или межсистемных.

3. Абсциссы основных направляющих точек при n=2 последовательно совпадают с целыми числами а и b в стандартных формулах – a²–b², 2ab и a²+b² – для нахождения пифагоровых троек.

3. Критическая точка, её положение и свойства

Критическая точка ограничивает зону начальной несовместимости (ЗНН) кривой и точек (рис.2-1, 2-2, 3-1). Для ЗНН, выделенной жирным прямоугольником на четырёх графиках рис.3-1 (n=4, n=8, n=9 и n=11), теорема Ферма доказывается достаточно легко.

Геометрический смысл ЗНН состоит в том, что первая прямая 1-й системы самых крутых параллельных линий, соединяющих точки, и кривая пересекаться не могут (рис.3-1). Вместе с тем, пересечение кривой и прямой 1-й системы является необходимым минимальным условием целочисленного решения радикала ⁿv[xⁿ+(x+С)ⁿ]; если на этом пересечении лежит точка, – подобное решение существует обязательно (при n=2). Если пересечения нет вообще, целочисленное решение ⁿv[xⁿ+(x+С)ⁿ] опять-таки исключается, и теорема для ЗНН доказана.

Невозможность пересечения доказывается решением неравенства. При любом показателе степени угловой коэффициент первой прямой 1-й системы, равный по условиям построения (ⁿv2)–1, больше углового коэффициента первого звена (и тем более других звеньев) ломаной линии, условно именуемой кривой (2-1). Угловой коэффициент первого звена кривой с х=1 определяется по (2-1), и неравенство решается не в его пользу (не в пользу кривой):

(ⁿv2)–1>C+1*(ⁿv2)–ⁿv[1ⁿ+(1+C)ⁿ] (3-1)

–1>C–ⁿv[1ⁿ+(1+C)ⁿ] и

ⁿv[1ⁿ+(1+C)ⁿ]>1+C

(последнее неравенство – очевидно). Кроме того, первая прямая 1-й системы является касательной к кривой с точкой касания в начале координат, и в дальнейшем эти две линии пересечься не могут. Формулой углового коэффициента касательной служит производная функции (2-1) – (2-12); подставляя в (2-12) х=0, независимо от показателя степени и параметра С получаем угловой коэффициент прямых 1-й системы параллельных линий: tg?_КСТ = (ⁿv2)–1=tg?_1-й.

Арифметический смысл ЗНН весьма прост. При небольших значениях абсциссы критической точки (х_КР) и, наоборот, больших значениях соотношения (х_КР+С)/х_КР роль второго слагаемого в подкоренном выраженииⁿv[x_КРⁿ+(x_КР+С)ⁿ] столь велика, что извлечение корня не позволяет получать числа, хотя бы на единицу больше, чем x_КР+С; таким образом, ограничениями величины радикала служит пара соседних членов натурального ряда, и целочисленное решение исключается:

x_КР+С < ⁿv[x_КРⁿ+(x_КР+С)ⁿ] ? х_КР+С+1 (3-2)

и при С=1 x_КР+1 < ⁿv[x_КРⁿ+(x_КР+1)ⁿ] ? х_КР+2 (3-3)

По условиям (3-2) и (3-3) абсцисса x_КР принимается, поскольку расчёту не поддаётся.

Критическая точка занимает определённое положение. Как было показано выше (3-1), пересечение первой прямой 1-й системы параллельных линий с кривой невозможно, но со второй по порядку прямой этой же системы оно неизбежно. Критическая точка находится непосредственно под этим пересечением (рис.3-1), а при n=2 – иногда – на пересечении. Выше кривой критическая точка не может находиться по условию (3-3). В этом случае величина радикала ⁿv[x_КРⁿ+(x_КР+1)ⁿ] больше, чем ближайшее целое число – х_КР+2, и критической становится предыдущая рядовая точка.

Имея представление о графической схеме в целом, о системах параллельных линий и их номерах, о ЗНН и ограничивающей её критической точке, целесообразно вернуться к разделу 2 для уточнения деталей. Уточнение, в частности, касается целой части десятичного числа (ЦЧДЧ) в формуле (2-2) взаимосвязи абсцисс и ординат всех точек (х; О):

О=х*(ⁿv2)–целая часть десятичного числа (ЦЧДЧ) (2-2)

Конкретизировав вычитаемое, получаем:

О=х*(ⁿv2)–х–(N–1), (3-4)

где N – порядковый номер прямой 1-й системы с рядовой точкой на ней.

Подставляя в (3-4) П_О/1=(ⁿv2)–1, получаем:

О=х*[(ⁿv2)–1]–(N–1)=х*П_О/1–(N–1) (3-5)

Поскольку порядковый номер прямой, на которой лежит критическая точка, – всегда второй (N=2), формула расчёта её ординаты (О_КР) далее упрощается до

О_КР=x_КР*П_О/1–1=x_КР*[(ⁿv2)–1]–1 (3-6)

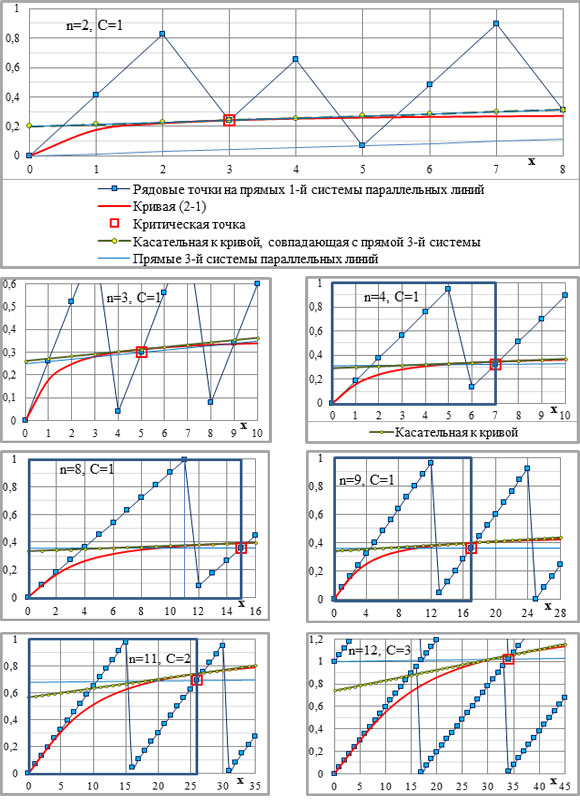
Рис.3-1. Положение критической точки относительно кривой (легенда – на верхнем и на втором сверху правом графике); показатель степени и параметр С – на графиках. На четырёх графиках (n=4, n=8, n=9 и n=11) жирным прямоугольником выделена зона начальной несовместимости (ЗНН) кривой и точек.

При n=2 критическая точка с абсциссой x_КР=3 входит в подмножество точек, ближайших и к кривой, и к нижнему горизонтальному ограничению элементарного графика. В подмножество точек, ближайших к его обоим горизонтальным ограничениям, входят все направляющие точки.

Графическая схема второй степени отличается максимальным размером первого приращения ординат – П_О/1 (рис.2-6). При n=2 оно больше предела кривой [см.(2-4)], и больше ординаты критической точки (рис.3-2-1 и 3-2-2).

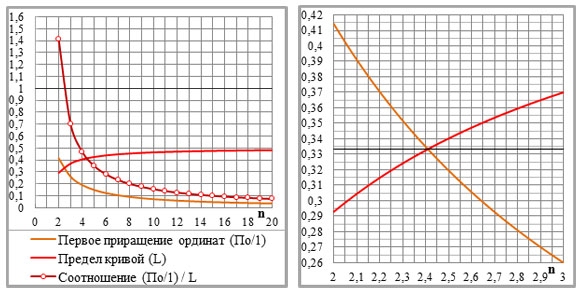
Рис.3-2-1. Соотношение первого приращения ординат – П_О/1 и предела кривой – L (П_О/1/L). Слева – основной график, справа – его фрагмент; легенда на основном графике.

При n=2 [(ⁿv2)–1]/[1–0,5(ⁿv2)] ? 1, при n? 2 [(ⁿv2)–1]/[1–0,5(ⁿv2)]?1

Решение уравнения (ⁿv2)–1=1–0,5(ⁿv2) определяет равновесный показатель степени: при n=ln2/ln(4/3)=2,40942 соотношение [(^2,40942v2)–1]/[1–0,5*(^2,40942v2)]=1, а его числитель и знаменатель равны 1/3 (см. правый график).

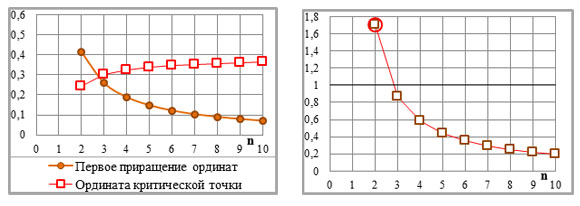
Рис.3-2-2. Соотношение первого приращения ординат – (ⁿv2)–1 – и ординаты критической точки – О_КР. Слева – значения параметров, справа соотношение [(ⁿv2)–1]/О_КР. Красный кружок при n=2 – единственное значение соотношения больше единицы.

Максимальным первым приращением ординат (П_О/1) при n=2 обусловлено минимальное число точек на прямых 1-й системы параллельных линий – две или три (верхние графики на рис.2-1, 3-1; прил.3-1-1). С максимальным первым приращением ординат связана и максимальная доля точек, ближайших к горизонтальным ограничениям графика. Доля этих точек в общем их количестве на элементарном графике равна удвоенному первому приращению ординат – 2*П_О/1. В результате – графическая схема второй степени располагает повышенным числом точек – потенциально направляющих. Потенциальная возможность, благодаря сплошной двоичности укрупняющих коэффициентов, реализуется в два подмножества направляющих точек (рис.2-4), а критическая точка приобретает дополнительный статус межсистемной направляющей точки.

Вертикальное расстояние между соседними точками на прямых линиях 1-й системы равно первому приращению ординат. Если оно больше предела кривой (рис.3-2-1), то больше любой её ординаты. Поэтому при n=2 все точки, лежащие на кривой или под ней, являются самыми нижними на прямых линиях 1-й системы (прил.3-1-1), то есть ближайшими к нижнему ограничению элементарного графика; критическая точка не является исключением. На кривой и под кривой точки вообще может не быть, только – над кривой. Наоборот, при n?2 ближайшие к кривой точки, включая критическую точку, из-за относительно малой величины первого приращения ординат (рис.3-2) на тех же прямых 1-й системы самыми нижними быть не могут (прил.3-1-2, 3-1-3).

Для характеристики критической точки определены а) предельное значение её абсциссы – в расчёте на единицу показателя степени и б) абсолютный предел её ординаты:

а) lim_n>? (х_КР/n)=(1/ln2)²=(Р_Г)²=2,0814 (3-7)

б) lim_n>? (O_КР)= (1/ln2)–1=Р_Г–1=0,4427 (3-8)

где Р_Г=1/ln2=1,4427 – предельное горизонтальное расстояние между прямыми 1-й системы параллельных линий – в расчёте на единицу показателя степени.

Далее уточняется положение критической точки относительно отрезков укрупнённых приращений ординат с двумя первыми порядковыми номерами (УП_О/1 и УП_О/2).

Формулы табл.2-1 позволяют представить абсолютное значение каждого отрицательного рядового приращения ординат, в том числе исходного (П_О/0=1), как сумму их последующих положительных укрупнённых приращений (УП_О), дополненную абсолютным значением одного рядового отрицательного [табл.3-1, (3-9а)]. Аналогичным способом можно представить абсолютное значение каждого положительного рядового приращения ординат, в том числе первого {П_О/1=[(ⁿv2)–1]}, как сумму их последующих отрицательных укрупнённых приращений, дополненную абсолютным значением одного рядового положительного [табл.3-1, (3-9б)].

Таблица 3-1

Представления приращений ординат (П_О/i) через последующие более мелкие приращения

Из табл.3-1 следует, что каждое отрицательное рядовое приращение ординат служит пределом суммы всех их последующих положительных укрупнённых приращений, соответствующих более пологим линиям, а каждое положительное рядовое приращение ординат является пределом суммы всех их последующих отрицательных УП_О. Таким образом, независимо от показателя степени, предел суммы положительных УП ординат при вовлечении в подсчёт всё более пологих восходящих линий на элементарном графике стремится к единице – исходному отрицательному рядовому приращению, а предел суммы отрицательных – к (ⁿv2)–1 – первому положительному рядовому приращению. Предел алгебраической суммы всех УП ординат (табл.3-2) – положительных и отрицательных – при С=1 равен (3-10):

lim ?_i=1^? (УП_О/i)=1–[(ⁿv2)–1]=2–(ⁿv2)=2*[1–0,5*(ⁿv2)] (3-10)

По аналогии с (2-5) предел алгебраической суммы УП ординат (УП_О) при неограниченном росте показателя степени имеет собственный предел: поскольку lim_n=2^? (ⁿv2)=1, то

lim_n>? [lim ?_i=1^? (П_О/i*УК_i)]=2*[1–0,5*(ⁿv2)]=2*(1–0,5*1)=1 (3-11)

Если при расчёте предела алгебраической суммы УП_О в (3-10) используются единица и П_О/1=(ⁿv2)–1, то в (2-4) – для расчёта предела кривой фигурируют половинки тех же величин.

Таблица 3-2

Предел алгебраической суммы укрупнённых приращений ординат и удвоенный предел кривой

	n=2			n=3			n=4
	ПО	УК	УПО	ПО	УК	УПО	ПО	УК		УПО
1	2	3	4	5	6	7	8	9		10
ПО/1	0,4142136	2	0,828427	0,2599211	3	0,779763	0,18920712	5		0,9460356
ПО/2	–0,171573	2	–0,34315	–0,220237	1	–0,22024	–0,0539644	3		–0,161893
ПО/3	0,0710678	2	0,142136	0,0396842	5	0,198421	0,02731384	1		0,0273138
ПО/4	–0,029437	2	–0,05888	–0,021816	1	–0,02182	–0,0266506	1		–0,026651
ПО/5	0,0121933	2	0,024387	0,0178684	1	0,017868	6,63255e–4	40		0,0265302
ПО/6	–0,005051	2	–0,01010	–0,003948	4	–0,01579	–1,2038e–4	5		–6,019e–4
ПО/7	0,0020920	2	0,004184	0,0020783	1	0,002078	6,13505e–5	1		6,1351e–5
ПО/8	–8,666e–4	2	–0,00173	–0,001869	1	–0,00187	–5,9030e–5	1		–5,903e–5
ПО/9	3,5894e–4	2	7,179e–4	2,0915e–4	8	0,001673	2,32013e–6	25		5,8003e–5
ПО/10	–1,487e–4	2	–2,97e–4	–1,960e–4	1	–1,96e–4	–1,0272e–6	2		–2,054e–6
ПО/11	6,1584e–5	2	1,232e–4	1,3144e–5	14	1,840e–4	2,65787e–7	3		7,9736e–7
ПО/12	–2,551e–5	2	–5,10e–5	–1,199e–5	1	–1,20e–5	–2,2981e–7	1		–2,298e–7
ПО/13	1,0566e–5	2	2,113e–5	1,1574e–6	10	0,000012	3,59756e–8	6		2,1585e–7
ПО/14	–4,377e–6	2	–8,75e–6	–4,129e–7	2	–8,26e–7	–1,3957e–8	2		–2,792e–7
Сумма нечётных УПО			0,999996			0,999999			0,99999999
Сумма чётных УПО			–0,41421			–0,25992			–0,1892071
Алгебраическая сумма			0,585784			0,740079			0,81079264
lim (ОКРВ)*2 при x>?			0,585786			0,740079			0,81079288
lim (ОКРВ) при x>?			0,292893			0,370039			0,40539644

Все приращения ординат – вертикальные проекции реально присутствующих на графиках отрезков прямых линий между точками. Реальные половинки отрезков укрупнённых приращений, ограниченные точками, присутствуют только тогда, когда они (УП_О) состоят из чётного числа рядовых приращений ординат (П_О). Пример «сплошной чётности», или «сплошной двоичности», демонстрируют укрупняющие коэффициенты (УКi=2) при n=2 (раздел 2). «Сплошная двоичность» УК предопределяет равенство предела алгебраической суммы бесконечного числа половинок УП_О, или что в этом единственном случае (при n=2) то же самое – предела суммы рядовых приращений ординат, реально присутствующих на графиках, пределу кривой:

0,5*lim ?_i=1^? (П_О/i*УК_i)=lim ?_i=1^? (П_О/i)=lim_х>?(О_КРВ) (3-12)

Если же при n>2 значение хотя бы одного УК нечётно, а в бесконечном ряду УК нечётных значений около 2/3, то в середине соответствующего укрупнённого приращения ординат (УП_О) точка отсутствует. Следовательно, на графике нет реальных половинок УП_О, алгебраическая сумма бесконечного числа которых могла бы соответствовать пределу кривой.

Равенство (3-12), реальное только при n=2, отражает срединное положение точек и предела кривой: точек – в том числе критической – в середине соответствующих отрезков УП_О (то есть наблюдается точечная симметрия), а предела кривой – в середине условного отрезка, высота которого равна алгебраической сумме бесконечного числа УП_О. При n?2, как показано ниже, срединное положение критической точки недостижимо.

От начала координат до предела кривой – бесконечное поле элементарного графика. Критическую же точку от начала координат отделяют в буквальном смысле слова два шага: первый шаг – вверх по первой прямой 1-й системы параллельных линий, соединяющих точки, второй шаг – вниз по одной из прямых 2-й системы (рис.3-3, 3-4).

При n=2 достигается полная гармония: первый шаг вверх – 0,5*УП_О/1 – приводит к точке перегиба над кривой, второй шаг вниз – 0,5*УП_О/2 – к критической точке точно на кривой. За пределами (ЗНН) – та же картина: половинки нечётных УП_О ведут вверх, к точке перегиба, половинки их чётных аналогов – вниз точно на кривую (рис.3-3).

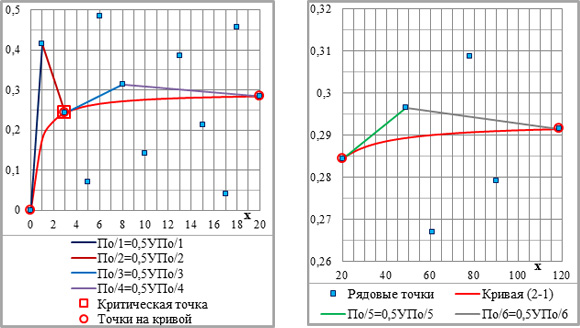
Рис.3-3. Положение точек на кривой и наклонных отрезках УП_О/i; n=2, С=1, УК_i=2.

При n>2 подобной гармонии нет, хотя существует вполне реальная вероятность, что двум первым шагам соответствуют чётный УК₁ и УК₂=2.

Критическая точка всегда лежит на второй по порядку прямой 1-й системы параллельных линий, соединяющих точки, и обязательным условием её срединного положения на отрезке УП_О/2 является равенство УК₂=2. Доля двойки в бесконечном ряду УК₂ при n>? составляет 1/6 [формула (2-10)]; доля чётных значений в бесконечном ряду УК₁ – 50%. Доля двух первых УК, отвечающих условиям срединного положения критической точки, составляет: 50%*(1/6)=1/12 (~8%). Таким образом, в ~92 случаях из ста, в частности, при показателях степени в интервале между n=2 и n=9 (рис.3-5), неравенство 0,5*УП_О/1–0,5*УП_О/2?О_КР обусловлено или нечётным УК₁, или неравенством – УК₂?2 (О_КР – ордината критической точки).

Более общая причина, полностью исключающая срединное (симметричное) положение критической точки при n?2, связана с нестандартной для первого укрупняющего коэффициента динамикой роста. При n>? УК₁ – в отличие от всех последующих УК_i (i ?1) – неограниченно растёт (рис.2-7); так же – в отличие от всех последующих УП_О/i, уменьшающихся с ростом показателя степени, – УП_О/1 скачкообразно растёт, стремится к единице (рис.2-6, правый верхний график), а 0,5*УП_О/1, соответственно, – к 0,5. Поскольку при этом вертикальная проекция отрезка УП_О/2 скачкообразно стремится к нулю, два шага по прямым линиям 1-й и 2-й систем параллельных линий с ростом показателя степени приводят нижние ограничения половинок УП_О/2 всё ближе и ближе к серединной горизонтальной линии элементарного графика – y=0,5 (рис.3-4).

Предел ординаты критической точки на 11% меньше, чем 0,5: 11%={1–[(1/ln2)–1]/0,5}*100% – [см. (3-8)], и её рост отстаёт от роста ординаты нижнего ограничения половинки УП_О/2. В результате уже при n=4 нижнее ограничение разности 0,5*УП_О/1–0,5*УП_О/2 находится выше критической точки, а при n?10 – даже выше предела её ординаты (рис.3-5).

При n?2 и УК₂=2 критическая точка может лежать в середине наклонных отрезков УП_А/2 и УП_О/2 (рис.3-4), но срединное положение их начальной точки – на первой прямой 1-й системы параллельных линий – недостижимо при любом показателе степени больше двух. Соответственно, исключается срединное положение критической точки в целом на отрезках двух первых укрупнённых приращений ( на нижнем ограничении разности 0,5*УП_О/1–0,5*УП_О/2).

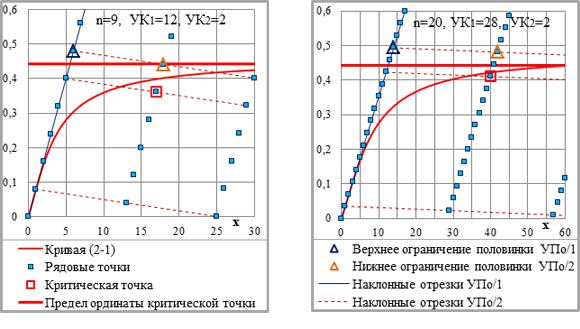
Рис.3-4. Положение критической точки на наклонных отрезках УП_О/1 и УП_О/2; показатели степени и укрупняющие коэффициенты – на графиках (легенда – на обоих графиках).

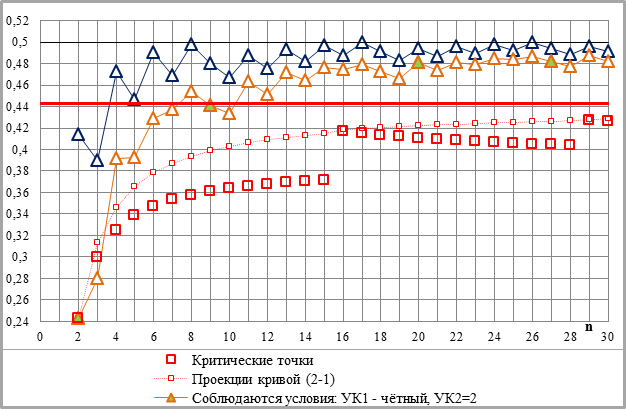
Рис.3-5. Фронтальная проекция ограничений отрезков укрупнённых приращений ординат (С=1). Часть легенды – на рис.3-4.

Выводы по разделу 3:

1) ни одна рядовая точка («последняя» точка) несовместима с пределом кривой и

2) срединное положение критической точки недостижимо при любом показателе степени больше двух.

4. Уникальные особенности графической схемы второй степени

Некоторые из этих особенностей требуют доказательства своей уникальности, в первую очередь – целочисленное решение радикала v[x²+(x+1)²] и графический аналог – совместимость кривой и точек; другие особенности – в наглядном изображении вполне очевидны, так же, как очевидно их отсутствие в графических схемах более высоких степеней. Наличие причинно-следственных связей между особенностями двух обозначенных групп облегчает общее доказательство теоремы и/или наглядно объясняет причины, обеспечивающие целочисленное решение радикала при n=2 и исключающие его при n?2.

Уникальные особенности графической схемы второй степени лежат в основе механизмов, позволяющих исключить негативное влияние несоизмеримости иррациональных чисел на совместимость кривой и точек, и тем самым обеспечить целочисленное решение радикала. Роль инструментов-параметров в составе этих механизмов отводится направляющим точкам – их координатам и тождественным им приращениям координат (см. ниже – через абзац).

Положению точек на кривой при n?2 препятствует несоизмеримость ординат двух (выделенных курсивом) главных элементов графической схемы. Отрезки несоизмеримы, если соотношение их длин иррационально. Но несоизмеримость иррациональных параметров не является всеобъемлющей. Соизмеримыми являются, в частности, рядовые и кратные им укрупнённые им приращения иррациональных ординат. Кроме того, если иррациональные числа – объекты простейших арифметических действий, например, вычитания, то уменьшаемое и вычитаемое вместе – в виде алгебраической суммы – равны полученной иррациональной разности и, разумеется, соизмеримы с ней. В формулах предлагаемой графической схемы – независимо от показателя степени – встречаются три типа разности и равенства иррациональных параметров.

I. Согласно (2-1), разность уменьшаемой суммы [1+х*(ⁿv2)] и вычитаемого радикала ⁿv[xⁿ+(х+1)ⁿ] равна ординате кривой (О_КРВ); согласно (2-2), дробная часть уменьшаемого при этом равна ординате точки [1+х*(ⁿv2)– целая часть десятичного числа]. Если на вертикали находится направляющая точка, разность её ординаты (О_НПР-i) с ординатами горизонтальных ограничений графика – О_НПР-i–0=П_О/i или 1–О_НПР-i+1=П_О/(i+1) – определяет дополнительный параметр – стандартное для каждого показателя степени приращение ординат, положительное и отрицательное, соответственно. Таким образом, направляющие точки в качестве источника (носителя) информации имеют преимущество перед рядовыми. Кроме того, их ординаты могут рассчитываться не только по (2-2), – как ординаты рядовых точек, но и по формулам табл.2-1, – как разность (алгебраическая сумма) иррациональных параметров (см. ниже – II и III типы).

II. Приращения ординат и абсцисс равны разности (алгебраической сумме) двух предыдущих приращений: рядового и укрупнённого (табл.2-1).

III. Координаты направляющих точки равны разности (алгебраической сумме) координат двух предыдущих направляющих точек с учётом укрупняющего коэффициента. Если в зоне начальной несовместимости (ЗНН)

П_А/3=П_А/1+УК₂*П_А/2 и П_О/3=П_О/1–УК₂*П_О/2, II тип (см. рис.2-2)

то х_НПР-3=х_НПР-1+УК₂*х_НПР-2 и О_НПР-3=О_НПР-1–УК₂*(1–О_НПР-2) III тип

Третий тип практически (арифметически) повторяет второй, так как все приращения координат равны координатам соответствующих направляющих точек. Выделение третьего типа в качестве самостоятельного связано с характеристикой критической точки. В ряде случаев аргументация относительно её позиции при различных показателях степени – n=2 или n?2 – с использованием координат выглядит не менее убедительно, нежели аналогичные доводы с использованием их стандартных приращений.

В графических схемах любой степени количество абсцисс точек (х) и радикалов в (2-1) бесконечно. Количество приращений координат (П_А/i и П_О/i) также бесконечно, но их бесконечность – меньшего порядка: приращения координат фиксируются только на вертикалях с направляющими точками, количество которых заметно уступает рядовым (рис.2-1, 2-4, 2-5).

Рядовые точки вписываются в равенства иррациональных параметров только I типа, изолированные (и реализуемые) в пределах одной вертикали. Направляющие точки, несущие дополнительную информацию о стандартных (единичных) приращениях, вписываются в равенства всех типов. Равенства II и III типа реализуются по наклонным – близким к горизонтальным – отрезкам укрупнённых приращений между двумя направляющими точками, в ЗНН – по отрезкам прямых 2-й системы параллельных линий (рис.4-1).

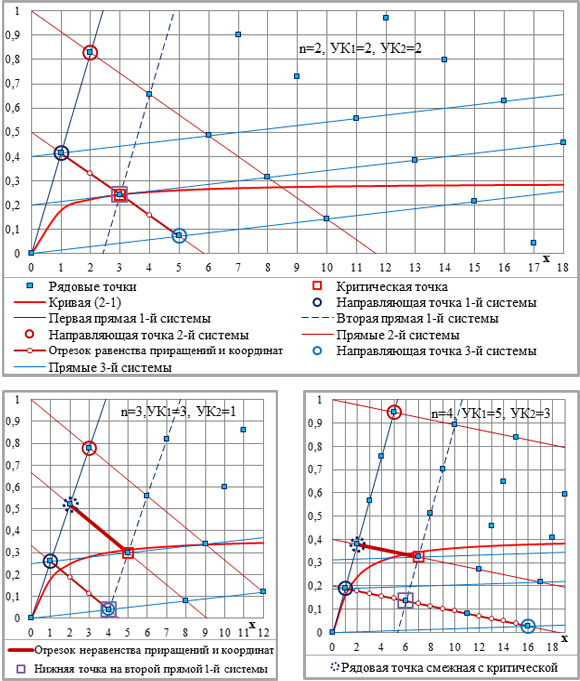
Рис.4-1. Графические элементы зоны начальной несовместимости (ЗНН); показатель степени и укрупняющие коэффициенты указаны на графиках; С=1. Легенда – на трёх первых графиках.

Независимо от показателя степени n сумма координат рядовой точки, смежной с критической, и направляющей точки 2-й системы параллельных линий равна координатам критической точки.

Независимо от показателя степени сумма координат направляющих точек 1-й и 2-й систем равна координатам (самой) нижней точки на второй прямой 1-й системы.

Только при n=2 совпадают друг с другом:

а) отрезки равенства и неравенства приращений и координат (при n=2 – только равенства),

б) критическая и самая нижняя точка на второй прямой 1-й системы,

в) направляющая точка 1-й системы и рядовая точка смежная с критической.

Продолжение рис.4-1.

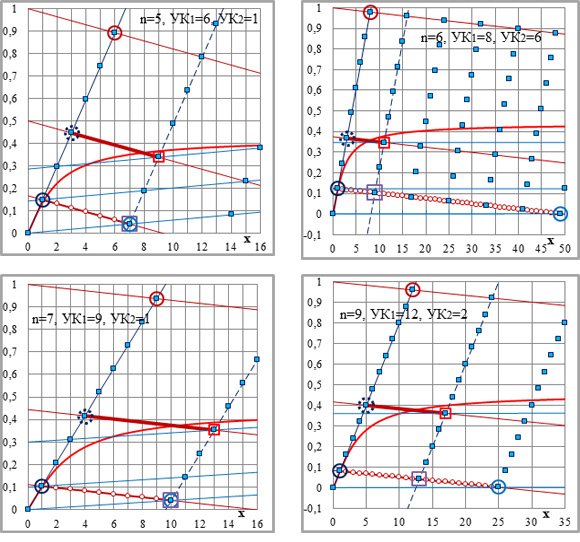
Таким образом, направляющие точки могут обеспечить равенство иррациональных параметров на определённой площади. Однако необходимые для этого условия создаются только в рамках графической схемы второй степени, благодаря её уникальным особенностям, и только в пределах ЗНН, где преимущество направляющих точек перед рядовыми реализуется в равенство алгебраической суммы нескольких приращений ординат и прироста ординаты кривой.

Первопричиной многих уникальных особенностей графической схемы второй степени является экстремальная – максимальная величина первого приращения ординат (рис.2-6). С ней, в частности, связано минимальное количество точек на первой прямой 1-й системы параллельных линий – две (рис.4-1), причём обе – направляющие. Критическая точка (с абсциссой х_КР=3) при n=2 одновременно служит межсистемной направляющей точкой (рис.2-1, 2-4, 2-5). В итоге графическая схема второй степени выгодно отличается полным отсутствием в ЗНН рядовых точек.

При n=2 на вертикалях х=1 и х=2 равенства I типа включают по одному рядовому приращению ординат – П_О/1 и П_О/2, которые в сумме с соответствующими радикалами равны ординате кривой (2-1) и соизмеримы с ней. Вместе с тем «поперечные» равенства II (и III) типа в ЗНН включают те же П_О/1 и П_О/2, которые в виде алгебраической суммы равны П_О/3 и соизмеримы с ним (табл.2-1, графа 2, строчка 3; рис.2-2). На вертикали х=3 ординату критической точки можно представить через всё те же два первых приращения ординат – П_О/1 и П_О/2 (и другими способами – табл.4-1, пп.2, 3, 4); в виде алгебраической суммы с положительной единицей и отрицательным радикалом она равна ординате кривой.

Таблица 4-1

Ордината критической точки (О_КР=0,242641) при n=2; (х_КР=3)

№№	(№№ формул)	Результат расчёта	Дробная часть
1	(3-6)	хКР*ПО/1–1=0,24264	0,242641
2	Табл.2-1, графа 2, строчка 3	ПО/1–ПО/2=ПО/1–0,5*УПО/2=0,24264	0,242641
3	Сумма ординат	ОНПР-1+ОНПР-2=ПО/1+2*ПО/1=1,24264	0,242641
4	Уменьшаемая сумма в (2-1)	1+хКР*v2=5,24264	0,242641
5	tg?3-й1) – (2-11)	0,2+хКР*tg?3-й=0,24264	0,242641
6	tg?КСТ1) – (2-12)	0,2+хКР*tg?КСТ=0,24264	0,242641

¹⁾ tg?_3-й=tg?_КСТ=v2–[3+(3+1)]/v[3²+(3+1)²].

Таким образом, на четырёх первых вертикалях, включая вертикаль х=0, на первой прямой 1-й системы и на отрезке УП_О/2 между 1-й и 3-й направляющими точками (рис.4-1) при n=2 – только равенства. Система вертикальных и наклонных линий, на которых реализуются соответствующие формулы, покрывает в пределах ЗНН всю площадь графика, а направляющие точки, включая межсистемную направляющую – критическую, органично вписываются в формулы. Прирост ординаты кривой соизмерим с приращениями ординат на отдельных вертикалях по формуле (2-1), а связку между вертикалями и соизмеримость приращений друг с другом обеспечивают формулы табл.2-1, 4-2 (и прил.4-1). Естественным образом для ЗНН создаётся уникальная возможность равенства приращений ординат (точек) и прироста ординаты кривой. При «сплошном» в ЗНН равенстве отклонение точки от кривой вверх первым положительным П_О/1 компенсируется вторым отрицательным П_О/2 вниз ровно настолько, чтобы точка на кривой в начале координат вновь вернулась на неё при х_КР=3 (П_О/1–П_О/2=П_О/1+П_О/3=О_КР).

Таблица 4-2 (см. также прил.4-1)

Равенства иррациональных параметров II и III типа в ЗНН при n=2

¹⁾ Координаты точки смежной с критической при n=2: х_{СМЖ_КР}=х_НПР-1; О_{СМЖ_КР}=О_НПР-1.

Преимущества графической схемы n=2 обнаруживаются и при сравнении координат точек в пределах ЗНН. При n=2 сумма абсцисс двух первых направляющих точек равна абсциссе критической точки:

х_НПР-1+х_НПР-2=1+2=3=х_КР=х_НПР-3–х_НПР-2=5–2=3 (4-1)

Уже при n=3 равенство (4-1) применительно к критической точке обращается в неравенство:

х_НПР-1+х_НПР-2=1+3=4?х_КР=5

и остаётся неравенством при n>? (прил.4-2); точка с ординатой, равной сумме ординат двух первых направляющих точек (за вычетом единицы), при этом смещается вниз и при любом показателе степени остаётся ближайшей к нижнему ограничению графика (рис.4-1). В отличие от графической схемы при n=2, подобное положение – у нижнего горизонтального ограничения графика – для критической точки при n?2 невозможно (раздел 3, прил.3-1-2, 3-1-3).

Сумма двух абсцисс – х_НПР-1 и х_НПР-2, первая из которых единица, может быть равна только абсциссе точки, непосредственно следующей за второй направляющей; при n=2 – это критическая точка. Уже с переходом от n=2 к n=3 между двумя первыми направляющими точками на первой прямой 1-й системы, а также между второй направляющей и критической точкой на второй прямой 1-й системы возникают интервалы (разрывы), заполняемые рядовыми точками, число которых с ростом показателя степени n непрерывно растёт. Сумма двух абсцисс – х_НПР-1 и х_НПР-2 – уравнивается с абсциссой не критической, а самой нижней точки (х_НЖН) на второй прямой 1-й системы – х_НЖН=х_НПР-1+х_НПР-2=1+УК₁ (прил.4-2, графа 5).

В результате равенство (4-1) остаётся неповторимым, то есть координаты критической точки при n?2 не могут быть равны сумме координат двух первых направляющих точек; иными словами, критическая точка не вписывается в равенства иррациональных параметров III типа.

Только при n=2 самая нижняя и критическая точки совпадают (рис.4-1; прил.4-2, графы 4, 5; прил.4-3, рис.4-3-1), и обе легко встраиваются в равенства II и III типа. Аналог равенства (4-1) для ординат (О_КР и О_НПР-i) при n=2:

О_НПР-1–(1–О_НПР-2)=О_КР=(1–О_НПР-2)+О_НПР-3 и в цифрах: (4-1а)

0,4142–(1–0,8284)=0,2426=(1–0,8284)+0,0710 (=M–M²=3M–1=M²+M³, где M=v2–1)

Проблему соизмеримости/несоизмеримости иррациональных параметров следует дополнить данными о возможном измерителе. Его выбор ограничен стандартными приращениями ординат: в виде алгебраической суммы какой-то их комбинации можно представить ординату любой точки; если критическая (или другая) точка лежит на кривой, её ордината должна быть представлена той же комбинацией приращений. Подобное совпадение происходит только при n=2.

Чем меньше измеритель, тем проще и точнее измерение. В формуле (3-6) используется самый крупный измеритель – П_О/1, – что не позволяет судить о структуре ординаты критической точки – О_КР и комбинациях слагающих её приращений. Структурные формулы (4-2) и (4-3), полученные в результате преобразований формул графы 2 табл.2-1, дают такую возможность. При n=2 коэффициент при самом крупном измерителе (П_О/1) обращается в единицу в (4-2) и ноль в (4-3):

О_КР=(x_КР–УК₁)*П_О/1–П_О/2 (4-2)

О_КР=[x_КР–(УК₁+1)]*П_О/1+(УК₂–1)*П_О/2+П_О/3 (4-3)

Независимо от показателя степени структурные формулы ординаты самой нижней точки (О_НЖН) на второй прямой 1-й системы (4-4) и (4-5) подобны (4-2) и (4-3), но коэффициенты при П_О/1 в них постоянны и неизменно равны единице и нулю, соответственно:

О_НЖН=П_О/1–П_О/2 (4-4)

О_НЖН=(УК₂–1)*П_О/2+П_О/3 (4-5)

Поскольку при n=2 самая нижняя и критическая точки совпадают, формулы (4-2) и (4-4) для этого показателя степени идентичны так же, как (4-3) и (4-5):

О_КР=(3-2)*П_О/1–П_О/2=П_О/1–П_О/2 (4-2) и (4-4)

О_КР=[3–(2+1)]*П_О/1+(2–1)*П_О/2+П_О/3=П_О/2+П_О/3 (4-3) и (4-5)

Что касается абсцисс, общая формула существует лишь для самой нижней точки на второй прямой 1-й системы параллельных линий:

х_НЖН=х_НПР-1+х_НПР-2=1+УК₁=1+2=3;

Только при n=2 абсцисса критической точки и протяжённость ЗНН – три единицы – совпадают с этими суммами (х_КР=х_НЖН=1+УК₁); при n?2 протяжённость ЗНН больше (х_КР?3).

Дело в том, что при растущем показателе степени темпы роста первого укрупняющего коэффициента (УК₁) определяются значением 1/ln2=1,443 (рис.2-7), тогда как темпы роста абсциссы критической точки (х_КР) – квадратом этой величины – (1/ln2)²=2,0814 [формула (3-7); прил.4-2, графы 3, 4].

В результате только при n=2 три звена ломаной линии – кривой (2-1) – соответствуют числу вертикалей ЗНН, объединяемых поперечными равенствами II и III типа по прямым второй системы параллельных линий. При n?2 те же равенства не охватывают в ЗНН все вертикали и не учитывают их данные, что исключает положение критической точки на кривой.

Несмотря на подобие формул и некоторые отмеченные выше повторения характеристик критической точки при n=2, самая нижняя точка на второй прямой 1-й системы при n?2 по ряду очевидных причин не может лежать на кривой (рис.4-1, прил.4-3).

К преимуществам графической схемы второй степени относится также уникальное положение критической точки. Она входит в подмножество точек, ближайших к кривой, и в то же время является ближайшей к нижнему горизонтальному ограничению графика.

Критическая точка при n=2 лежит на «отрезке равенства приращений и координат», – на самой нижней прямой 2-й системы параллельных линий – между 1-й и 3-й направляющими точками (рис.4-1). Смежная с ней 1-я направляющая точка на первой прямой 1-й системы лежит между началом координат и 2-й направляющей точкой.

Будучи в подобном окружении, критическая точка легко вписывается в систему равенств иррациональных параметров II и III типа (табл.4-2, прил.4-1). Благодаря сплошной двоичности укрупняющих коэффициентов, формулы табл.2-1 также легко делятся на две равные части, фиксируя критическую и смежную с ней точку в середине отрезков укрупнённых приращений координат – УП_А и УП_О – двух первых систем.

При n?2 критическая точка лежит на «отрезке неравенства приращений и координат», – выше аналогичного «отрезка равенства», соединяющего 1-ю и 3-ю направляющие точки (рис.4-1). Точка, смежная с критической, на первой прямой 1-й системы – рядовая (при n=2 – направляющая). В соответствии со вторым выводом раздела 3 срединное положение критической точки недостижимо при любом показателе степени больше двух, что исключает возможность симметрично встроить её в систему равенств иррациональных параметров II и III типа.

Существует ещё один вариант объяснения причин положения критической точки на кривой при n=2.

При расчётах членов ряда радикалов ⁿv[хⁿ+(х+1)ⁿ] с ростом абсциссы х на единицу его целая часть в большинстве случаев увеличивается на ту же единицу (при любом показателе степени). Но когда разность дробной части радикала и ближайшего целого числа становится меньше (ⁿv2)–1, целая часть радикала с ростом х на единицу нестандартно прирастает двойкой (табл. к рис.4-2).

Критическая точка и другие точки, лежащие на кривой при n=2, а также ближайшие к ней точки при n?2 обязательно приурочены к нестандартным отрезкам; при n=2 упомянутые точки находятся на их окончании, при n?2 – на любой позиции (рис.4-2).

Из-за максимального значения первого приращения ординат нестандартные отрезки при n=2 не всегда умещаются под кривой, и их начальная часть находится у верхнего ограничения элементарного графика, на предыдущей – первой прямой 1-й системы. Верхнее горизонтальное ограничение – y=1 – отсекает от нестандартных отрезков части, точно соответствующие чётным приращениям ординат, – если точка в конце нестандартного отрезка лежит на кривой. Все приращения ординат определяются через два исходных приращения – ⁿv2 и единицу; поэтому, несмотря на иррациональные значения, они соизмеримы друг с другом: каждое из них равно алгебраической сумме двух предыдущих – рядового и укрупнённого (табл.2-1, графа 2). У нестандартного отрезка с критической точкой в конце его верхняя часть равна П_О/2, нижняя – П_О/1–П_О/2=П_О/2+П_О/3. Последующие подобные отрезки сложены иными комбинациями приращений ординат (рис.4-2 с табл.), но так же соизмеримы друг с другом и с предыдущими приращениями.

При n?2 нестандартные отрезки не пересекаются горизонтальными ограничениями графика, но пересекаются – делятся на две части кривой (рис.4-2).

Связь между уникальными особенностями графической схемы второй степени, не требующими доказательства своей уникальности, очевидна: экстремальная – максимальная величина первого приращения ординат обусловливает и отсутствие в ЗНН рядовых точек, и оптимальное положение критической точки, и соответствие протяжённости ЗНН сумме УК₁+1 и абсциссе самой нижней точки на второй прямой 1-й системы параллельных линий. Достаточно очевидна также связь между двумя группами уникальных свойств: положение критической точки на «отрезке равенства приращений и координат» позволяет встроить её в формулы (4-1), (4-1а) и табл.4-2 (графа 3). Из-за сдвига критической точки вверх, на аналогичный «отрезок неравенства», названные формулы неповторимы при n?2, что исключает в пределах ЗНН возможность равенства приращений ординат (точек) и прироста ординаты кривой.

Благодаря вышеперечисленным преимуществам графической схемы при n=2, соизмеримость иррациональных приращений ординат и радикалов в (2-1) при n=2 реализуется не только на отдельных вертикалях – по I типу, но и на отрезках укрупнённых приращений координат двух первых систем параллельных линий – по II и III типу (табл.4-1). Объединённая реализация равенств иррациональных параметров всех типов обеспечивает в ЗНН при n=2 равенство приращений ординат (точек) и прироста ординаты кривой.

Описание преимуществ и ограничений графических схем при n=2 и n?2, соответственно, продолжается далее уточнением механизмов, обеспечивающих совместимость кривой и точек.

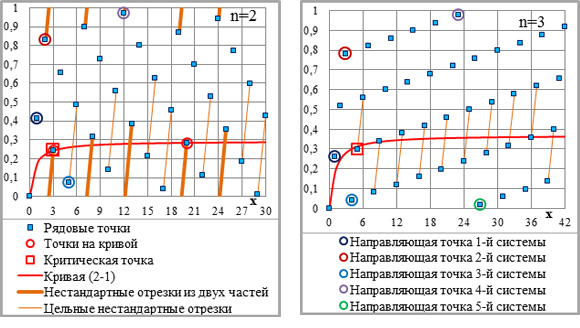
Рис.4-2. Нестандартные отрезки между соседними точками; для нестандартных отрезков рост аргумента – абсциссы «х» – на единицу приводит к приросту целой части радикала v[xⁿ+(х+1)ⁿ] на два пункта. Слева n=2, справа n=3. Легенда на обоих графиках.

Таблица к рис.4-2

Вертикальные проекции нестандартных отрезков (при n=2),

состоящих из двух частей [М=(v2)–1]

Абсциссы точек:		Нестандартные отрезки из двух частей 1)
соседних точек	точек пересеч.2)	Верхняя часть	Нижняя часть
1	2	3	4=М–3
2-3	2,414214	М2=1–2М=0,17157288	М–М2=М2+М3=0,24264069
7-8	7,242641	М2–М3=М3+М4=0,1005051	М–М3–М4=М2+2М3=0,31370850
12-13	12,07107	М4=М2–2М3=0,02943725	М–М2+2М3=2М2+М3–М4=0,38478
19-20	19,31371	М3+2М4=М2–М3+М4=0,12994	М–М3–2М4=М2+М3+М4+М5=0,284
24-25	24,14214	М3–М5=2М4=0,058874503	М–2М4=М2+2М3+М4+М5=0,3553
…	…	…	…
…	…	…	…
118-119	118,296465	4М4+М6=М3+М4+М5+2М6=0,1228	М–4М4–М6=М2+М3+М4+М5+М6+М7

¹⁾ Возможны иные варианты приведенных в таблице алгебраических сумм.

²⁾ Точки пересечения нестандартных отрезков с горизонтальными ограничениями графика.

Изложенные причины а) равенства суммы приращений ординат (точек) и суммарного прироста ординаты кривой в пределах ЗНН, а также б) положения критической точки на кривой и целочисленного решения радикала v[х_КР²+(х_КР+1)²] – не следует считать основными. Скорее всего, это равенство – следствие комплекса причин, среди которых трудно выделить первую –основную. Подобным же следствием, но не причиной, является равенство угловых коэффициентов прямой 3-й системы параллельных линий и касательной к кривой в точке с абсциссой, равной абсциссе критической точки (табл.4-1, пп.5, 6).

Описанные выше уникальные свойства графической схемы второй степени создают благоприятные условия. Конкретным же механизмом, обеспечивающим целочисленное решение радикала, служит естественное совпадение абсцисс направляющих точек – х_НПР-1=1 и х_НПР-2=2 с целыми числами а и b в стандартных формулах нахождения пифагоровых троек – a²–b², 2ab и a²+b². Разность квадратов определяет первое число первой пифагоровой тройки – абсциссу критической точки – х_КР=b²–a²=2²–1²=3, а сумма квадратов – третье число тройки – абсциссу 3-й направляющей точки – х_НПР-3=b²+a²=2²+1²=v[3²+(3+1)²]=5 (табл.2-3, строчка 1).

Ордината кривой по (2-1) – рассчитывается нарастающим итогом, и вертикальный отрезок между критической точкой и кривой зависит только от последнего радикала. Если сумма квадратов (х_КР=b²+a²) уже определила радикал в виде целого числа, то суммарный прирост ординаты кривой в пределах ЗНН по (2-1) – О_КРВ=1+х*(ⁿv2)–v[х²+(х+1)²] – автоматически уравнивается с суммой приращений ординат (точек) – х*(ⁿv2)–целое число, то есть с дробной частью уменьшаемого в (2-1) (табл.4-1, п.4). Так же при целочисленном радикале в знаменателе вычитаемого в (2-12) уравниваются угловые коэффициенты прямой 3-й системы параллельных линий и касательной к кривой в точке с абсциссой, равной абсциссе критической точки (то есть при х_КСТ=х_КР).

Даже в рамках графической схемы второй степени непосредственное соседство двух направляющих точек при равенстве суммы их координат (суммы ординат – за вычетом единицы) координатам точки на кривой – уникально. Подобное соседство возможно лишь в ЗНН, на первой прямой 1-й системы параллельных линий; наряду с уникальным положением критической точки, оно способствует её попаданию на кривую и целочисленному решению радикала.

За пределами ЗНН необходимость непосредственного соседства двух направляющих точек не обязательна, так как возможность целочисленного решения радикала и совместимость с кривой точек с другими абсциссами (х=20, х=119, х=696 и т.д. – рис.3-3; прил.4-4) обусловлены иными причинами.

Во-первых, за пределами ЗНН абсциссы направляющих точек, по-прежнему, как и в ЗНН играя роль целых чисел а и b, по формулам a²–b² или 2ab бесконечно генерируют абсциссы точек на кривой, а по формуле a²+b² – воспроизводят абсциссы направляющих точек нечётных систем параллельных линий (табл.2-3; прил.4-4).

Во-вторых, кривые (2-1) относятся к типу эллиптических кривых, которые обладают свойством воспроизводить целочисленные точки на пересечении с хордами, проведенными из начала координат и параллельными касательным в предыдущих целочисленных точках. Обязательным условием реализации сформулированного свойства является наличие на эллиптической кривой первой точки с целочисленной абсциссой. При n=2 это критическая точка (можно считать её обязательной второй точкой, при первой, которая независимо от показателя степени лежит на кривой в начале координат).

Две названные причины, вероятно, дополняют друг друга.

Причины совместимости точек с кривой в ЗНН и за её пределами несколько отличаются друг от друга, но механизм – одинаковый: прирост ординаты кривой, необходимый для попадания на неё какой-либо точки, формируется на вертикали, предшествующей этой точке. В частности, параметры второй вертикали при n=2 достаточны, чтобы рассчитать прирост ординаты кривой на один шаг вперёд, – между вертикалями х=2 и х=3 (0,01976 – прил.4-5).

В рамках графической схемы второй степени для расчёта абсциссы очередной точки на кривой абсцисса предыдущей аналогичной точки (в ЗНН – ноль в начале координат) суммируется с абсциссами двух направляющих точек, расположенных между двумя упомянутыми точками на кривой – предыдущей и очередной (прил.4-4, табл.4-4-1).

При n?2 даже одна рядовая точка нарушает «сплошное» равенство на площади ЗНН. Присутствие рядовых точек не препятствует реализации вертикальных равенств иррациональных параметров I типа. Но их поперечные равенства II и III типа, реализуемые по прямым 2-й системы параллельных линий или включают не критическую, а самую нижнюю точку на второй прямой 1-й системы, или не охватывают все вертикальные равенства I типа.

Между вертикалью с рядовой точкой и предыдущей вертикалью – независимо от того, маркирована ли она рядовой или направляющей точкой, – прирост ординаты кривой несоизмерим со стандартными единичными приращениями ординат. Первая рядовая точка появляется в ЗНН на первой прямой 1-й системы параллельных линий уже при n=3, и в дальнейшем, при последующем росте показателя степени количество рядовых точек также растёт, что предопределяет несовместимость критической точки и кривой.

Несовместимость не ограничивается критической точкой. За пределами ЗНН компенсировать её отклонение от кривой невозможно; компенсирующими отрезками могут служить лишь единичные стандартные приращения ординат, однако они реально присутствуют на графике лишь на редких вертикалях с направляющими точками.

Вывод относительно несовместимости точек и кривой за пределами ЗНН возможен также на базе разности и равенства иррациональных параметров III типа.

Если координаты критической точки не равны сумме координат двух первых направляющих точек, то никакая другая точка не попадёт на кривую: её координаты уже не могут быть алгебраической суммой координат всех предыдущих направляющих точек. Наоборот, при n=2 координаты любой точки на кривой равны сумме координат всех предыдущих направляющих точек (рис.4-1, прил.4-4).

Вывод по разделу 4. Преимущества графической схемы второй степени – минимальная протяжённость ЗНН, отсутствие в ней рядовых точек с ограниченной информацией, уникальное положение критической точки и другие, – обусловленные аномально большой величиной первого приращения ординат (рис.2-6), – определяют коренное различие всех параметров при n=2 и n?2. Названные преимущества на графиках рис.4-1 очевидны и их доказательства не требуется. Предложенная схема позволяет наглядно объяснить совместимость критической точки с кривой при n=2 и их несовместимость – при n?2.

После подобного вывода следовало бы закончить работу, но упомянув о принадлежности кривых к типу эллиптических, необходимо, во-первых, обосновать её (прил.4-6) и, во-вторых, показать связанные с эллиптическими кривыми возможности – в виде схем общего доказательства теоремы (прил.4-7).

Перечень уникальных особенностей графической схемы второй степени

Повторим, что некоторые из особенностей графической схемы второй степени требуют доказательства своей уникальности, другие вполне очевидны.

В первую группу входят:

1. Целочисленное решение радикала v[x²+(x+С)²] – собственно теорема Ферма.

2. Совместимость кривой и точек, в том числе – критической (графический аналог теоремы).

3. Совпадение касательных в целочисленных точках на кривой, в том числе в критической точке, с прямыми, входящими в системы параллельных линий с нечётными порядковыми номерами.

4. Связь координат обычных и межсистемных направляющих точек (прил.2-1).

5. Кратность угловых коэффициентов прямых 1-й системы параллельных линий, соединяющих точки, прямому углу: tg ( 90?/4)=v2–1=0,414214.

Во вторую группу входят вполне очевидные особенности графической схемы при n=2, отсутствие которых при n?2 не требует доказательства.

6. Сплошная двоичность укрупняющих коэффициентов; в бесконечном ряду показателей степени при n?2 теоретически все укрупняющие коэффициенты могут быть двойками, кроме первого: УК₁=2 только при n=2 (рис.2-7).

7. Наличие двух комплектов систем параллельных линий и двух подмножеств направляющих точек – основных и межсистемных (рис.2-4, 2-5).

8. Равенство всех рядовых приращений ординат абсолютным значениям последовательно растущих степеней их первого приращения (табл.2-2)

9. Совпадение абсцисс направляющих точек с целыми числа а и b в стандартных формулах нахождения пифагоровых троек (табл.2-3).

10. Максимальная величина первого приращения ординат по сравнению с его значениями при показателях степени больше двух [(v2)–1]?[(ⁿv2)–1] (рис.2-6).

11. Соотношение первого приращения ординат и предела кривой больше единицы (рис.3-2-1).

12. Соотношение первого приращения ординат с ординатой критической точки больше единицы (рис.3-2-2).

13. Срединное положение критической точки на границе зоны начальной несовместимости (ЗНН) – на отрезках двух первых укрупнённых приращений ординат (рис.3-3).

14. В ЗНН присутствуют только направляющие точки и отсутствуют рядовые (рис.4-1).

15. Совпадение критической и самой нижней точки на второй прямой 1-й системы параллельных линий, соединяющих точки (рис.4-1).

16. Координаты критической точки равны сумме координат двух первых направляющих точек [равенство (4-1) для абсцисс и его аналог для ординат (4-1а)].

17. Соответствие протяжённости ЗНН сумме УК₁+1

5. Заключение

В качестве заключения приводится ретроспективное изложение последовательности проведенных исследований. В них можно условно выделить два частично перекрывающих друг друга этапа: разработку графической схемы и её использование.

Исследования заранее не планировались. В условиях полной неопределённости и отсутствия каких-либо идей «методика» работ на начальной стадии сводилась к массовым расчётам радикала ⁿv[xⁿ+(x+С)ⁿ] при различных показателях степени n, растущем значении х и параметре С, в основном равным единице. В дальнейшем результаты каждой стадии исследований каждый раз подсказывали их направление на следующей стадии.

В большинстве случаев рост х на единицу приводит к приросту целой части радикала на ту же единицу (при С=1). Но когда разность дробной части радикала и ближайшего целого числа становится меньше (ⁿv2)–1, целая часть радикала прирастает двойкой; частота подобной смены уменьшается с ростом показателя степени. Из этих наблюдений возник интерес к дробной части радикала, определилось значение первого приращения ординат [(ⁿv2)–1], и началось массовое построение графиков точек с координатами [x; х*(ⁿv2)–целая часть десятичного числа].

Далее было установлено, что упомянутая выше смена единиц на двойку происходит между двумя точками в нижней части графиков, на всей их протяжённости. Наметилась невидимая граница, делящая графики на две неравные части. Простейшими действиями с рядами радикалов эта граница материализовалась в кривую (2-1).

Объединение точек и кривой на одном графике сразу позволило выявить разницу графических схем при n=2 и n?2, найти наглядный признак целочисленного решения радикала и, соответственно, по новому сформулировать теорему: кривая и точки с указанными выше координатами несовместимы при показателях степени больше двух.

Развитие графических схем привело к соединению точек параллельными линиями, объединяемыми в системы с чётными и нечётными порядковыми номерами; системы линий постепенно «обрастали» характерными параметрами – рядовыми и укрупнёнными приращениями абсцисс и ординат, угловыми коэффициентами. Для расчёта приращений координат (табл.2-1) потребовались укрупняющие коэффициенты (УК). Среди точек сначала выделились рядовые, затем направляющие – первые на первых (направляющих) прямых каждой системы и ближайшие к горизонтальным ограничениям элементарного графика. Уникальность графической схемы второй степени получала новые подтверждения – в виде постоянства отношений соседних приращений ординат [(2-9а) и (2-9б)] и «сплошной» двоичности УК (прил.4-4, табл.4-4-3, графы 2 и 4 – УК_i=2 выделены жирным шрифтом).

Использование формирующейся графической схемы постепенно стало давать результаты. В соответствии с признаком целочисленного решения радикала его минимальным условием является пересечение кривой и какой-либо прямой 1-й системы параллельных линий, соединяющих точки. На графиках кривой отчётливо наблюдается невозможность её пересечения с первой прямой 1-й системы (3-1), – так определились зона начальной несовместимости (ЗНН) и ограничивающая её критическая точка с характерным положением ниже кривой на второй прямой 1-й системы.

Если кривая (2-1) разделила график на нижнюю и верхнюю часть, то критическая точка – на бесконечную правую и «ограниченно-бесконечную» левую (или – бесконечную намного меньшего порядка). Есть и другое различие: протяжённость правой части бесконечна независимо от показателя степени n, левой – ЗНН – бесконечна лишь при n>?, но при небольших значениях n – конечна и полностью умещается на графиках. Монотонный элементарный график приобрёл в виде критической точки осязаемый ориентир, а ЗНН стала оптимальным участком для общего доказательства теоремы.

Дело в том, что доказательные схемы в правой части выглядят неубедительно, так как предполагают использование предельных значений некоторых параметров, недосягаемых для любой функции по определению.

Так, по причине недостижимости предела кривой и неопределённости положения «последней» рядовой точки – не выдерживает критики утверждение о несовместимости двух выделенных курсивом элементов графика (раздел 3).

Из-за сомнений в возможности применения предельных значений пришло понимание, что ЗНН, – открытая для наблюдений при небольших показателях степени и характеризующаяся конкретными значениями параметров, – предпочтительнее для доказательства теоремы, чем правая часть графиков.

Последовало более детальное исследование ЗНН, опять-таки выявившее существенные различия графических схем при n=2 и n?2. Ключевой уникальной особенностью графической схемы второй степени – не по существу, а для решения задачи – стало отсутствие в ЗНН рядовых точек и присутствие – только направляющих. Необходимо было решить, в чём преимущество вторых над первыми; со временем удалось установить, что дело в более конкретной, определённой, однозначной информации, несущей направляющими точками.

Возник новый вопрос относительно механизма реализации преимущества направляющих точек. Подсказкой для решения стала уникальная позиция критической точки – на «отрезке равенства приращений и координат», в самой нижней части второй прямой 1-й системы параллельных линий (рис.4-1), – позволяющая вписать (встроить) её параметры в канонические для предложенной графической схемы уравнения табл.2-1 и 4-2. Объяснив причины и следствия положения критической точки на кривой, стало возможным объяснение иной её позиции. При n?2 рядовые точки с размытой, неопределённой информацией – сразу о нескольких приращениях ординат – сдвигают критическую точку вверх – на «отрезок неравенства приращений и координат», – и её параметры уже не вписываются в уравнения указанных выше таблиц. Тем самым исключается возможность совместимости точек и кривой.

Схема доказательства несовместимости точек и кривой при n?2 (в разделе 4) на базе уникальных особенностей графической схемы при n=2 отчасти напоминает доказательство «по прецеденту» (или – «вопреки прецеденту»), применяемому в юридической практике некоторых стран. Используемый в настоящей работе ответственный термин «доказательство» вполне возможно заменить менее претенциозным понятием «объяснение» (например, «объяснение причин, обеспечивающих целочисленное решение радикала ⁿv[xⁿ+(x+1)ⁿ] при n=2 и исключающих его при n?2»).

Многочисленные методологические требования предлагают сформулировать в заключении к научной работе обоснование её основных результатов. В настоящем исследовании обоснованием многих результатов служат достаточно простые графики. В частности, применительно к доказательству несовместимости критической и других точек с кривой в качестве главного обоснования выступают графики рис.4-1, на которых вполне отчётливо и без возможности двойного толкования видна кардинальная разница различных элементов и позиций в графических схемах при n=2 и n?2. Разница по перечисленным ниже трём главным элементам и позициям рис.4-1 настолько наглядна и очевидна, что нет необходимости доказывать её существование.

1. При n=2 в ЗНН рядовые точки отсутствуют, при n?2 – присутствуют, причём с ростом показателя степени графической схемы их количество в ЗНН только увеличивается.

2. При n=2 критическая точка – самая нижняя на второй прямой 1-й системы параллельных линий, соединяющих точки; при n?2 она – не самая нижняя, сдвинута вверх, и её параметры уже не вписываются в уравнения табл.2-1 и 4-2. Тем самым исключается возможность совместимости точек и кривой и целочисленное решение радикала.

3. При n=2 протяжённость ЗНН равна сумме УК₁+1 (3=3). При n?2 протяжённость ЗНН больше указанной суммы; с ростом показателя степени это несоответствие усугубляется, из-за чего равенства II и III типа не охватывают в ЗНН все вертикали и не учитывают их данные, что исключает положение критической точки на кривой.

Таким образом, наглядное изображение теоремы Ферма в виде разнообразных графиков не только иллюстрирует текст, но и обосновывает его основные выводы.

И.И. Лещенко

Список приложений

№№	Название разделов и приложений
	1. Введение
	2. Общая характеристика графической схемы
2-1	Абсциссы точек, как пары числа a и b для нахождения пифагоровых троек.
	3. Критическая точка, её положение и свойства
3-1	Положение точек, лежащих на кривой (n=2, С=1) и ближайших к ней (n=3, 4; С=1), на прямых линиях 1-й системы
	4. Уникальные особенности графической схемы второй степени
4-1	II и III типы равенства иррациональных параметров в ЗНН при n=2 и УКi=2
4-2	Координаты точек на первой и второй прямой 1-й системы параллельных линий
4-3	Сравнение параметров критической точки при n=2 и самой нижней точки при n?2 на второй прямой 1-й системы параллельных линий, соединяющих точки
4-4	Варианты расчёта координат точек при n=2
4-5	Суммарные приращения ординат точек и прирост ординаты кривой в ЗНН при n=2
4-6	Обоснование принадлежности кривых к типу эллиптических
4-7	Схемы общего доказательства теоремы Ферма

Приложение 2-1

Абсциссы точек, как пары числа a и b для нахождения пифагоровых троек. Жирным шрифтом в графе 2 выделены абсциссы направляющих точек (х_НПР), курсивом – абсциссы межсистемных направляющих точек (х_М/С). Ординаты точек О_НПР=х_НПР*(v2)–БЦ

или О_М/С=х_М/С*(v2)–БЦ {M=[(v2)–1]}

Параметр С можно рассчитать, как абсолютное значение разности двух первых чисел троек – С=¦b²–a²–2ab¦ или по формуле разности квадратов (2-1-1):

С=[х_НПР*(v2)–БЦ]*[х_НПР*(v2)+БЦ]=[х_НПР*(v2)] ²–БЦ ² (2-1-1)

где БЦ – ближайшее к произведению х_НПР*(v2) целое число, равное абсциссе соседней межсистемной направляющей точки – БЦ=х_М/С (табл.2-1-1, графы 2, 4).

Подставив в (2-1-1) х_НПР=(О_НПР+БЦ)/(v2) [см. формулу (2-2) в тексте], и разделив обе части равенства на О_НПР, – получаем формулы связи координат обычных и межсистемных направляющих точек – (2-1-2) и (2-1-2₁):

С/О_НПР=2*БЦ+О_НПР (2-1-2);

и при С=1: 1/О_НПР=2*БЦ+О_НПР или 1/О_НПР=2*х_М/С+О_НПР (2-1-2₁)

Таблица 2-1-1

Характер связи между приращениями абсцисс и ординат при n=2 и С=1 {M=[(v2)–1]}

Равенство дробных частей – {1/[(v2)–1]ⁱ}={[(v2)–1]ⁱ} или {1/[(v2)–1]ⁱ}={1–[(v2)–1]ⁱ} – скорее всего, уникально, но его отсутствие при n?2 требует отдельного доказательства. При n?2 формула (2-1-1) не действует – не известны формулы разности кубов и разности более высоких степеней; нет и механизма обратной связи координат направляющих точек (2-1-2).

Приложение 3-1-1

Положение точек, лежащих на кривой и на прямых линиях 1-й системы (n=2, С=1).

Легенда – на всех графиках.

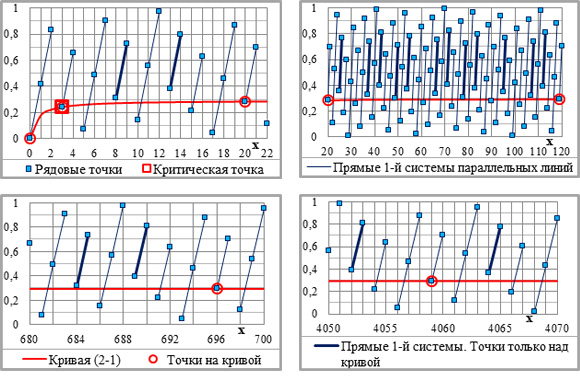
Приложение 3-1-2

Положение точек, ближайших к кривой и лежащих на прямых линиях 1-й системы (n=3, С=1).

Легенда – в прил.3-1-1 и на левом графике.

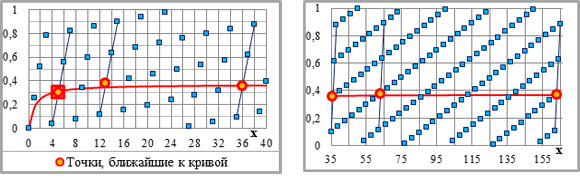
Приложение 3-1-3

Положение точек, ближайших к кривой и лежащих на прямых линиях 1-й системы (n=4, С=1).

Легенда – в прил.3-1-1 и 3-1-2.

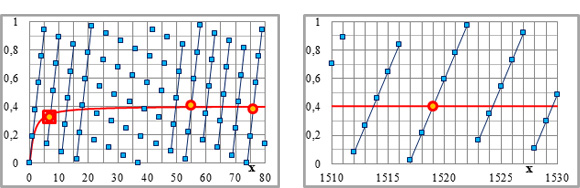
Приложение 4-1

II и III типы равенства иррациональных параметров в зоне начальной несовместимости (ЗНН)

при n=2 и УК_i=2

¹⁾ Типы разницы и равенства иррациональных параметров (см. текст, раздел 4).

²⁾ Координаты точки смежной с критической (рис.4-1); при n=2 х_{СМЖ_КР}=х_НПР-1 и О_{СМЖ_КР}=О_НПР-1.

Приложение 4-2

Координаты¹⁾ точек на первой и второй прямой 1-й системы параллельных линий.

В последней строчке – предельное соотношение данных графы с показателем степени (С=1).

n	Абсциссы (х)				Разница3)
	Первая прямая 1-й системы		Вторая прямая 1-й системы
	1-я направляющая точка (хНПР-1=1)	2-я направляющая точка (xНПР-2=УК1)	Критическая точка (xКР)	Самая нижняя точка2) (xНЖН)
1	2	3	4	5=2+3	6=4–5
2	1	2	3	3	0
3	1	3	5	4	1
4	1	5	7	6	1
5	1	6	9	7	2
6	1	8	11	9	2
7	1	9	13	10	3
8	1	11	15	12	3
9	1	12	17	13	4
10	1	13	19	14	5
11	1	15	21	16	5
12	1	16	23	17	6
45	1	64	92	65	27
50	1	71	102	72	30
10001	1	14427	20781	14428	6353
10002	1	14429	20783	14430	6353
10003	1	14430	20785	14431	6354
10004	1	14432	20787	14433	6354
10005	1	14433	20790	14434	6356
?	0	1/ln2=1,442695	(1/ln2)2=2,0814	1/ln2=1,442695	0,63867 3)

¹⁾ Приводятся только абсциссы; ординаты точек могут быть рассчитаны по формуле (2-2).

²⁾ Сумма абсцисс 1-й и 2-й направляющих точек равна абсциссе самой нижней точки (х_НЖН=х_НПР-1+х_НПР-2=УК₁+1).

³⁾ Разница абсциссы критической точки и суммы абсцисс 1-й и 2-й направляющих точек [x_КР–(УК₁+1)]; предел разницы равен [(1/ln2)²–1/ln2]=0,63867.

Приложение 4-3

Сравнение параметров критической точки при n=2 и самой нижней точки при n?2 на второй прямой 1-й системы параллельных линий, соединяющих точки

Независимо от показателя степени самая нижняя точка на второй прямой 1-й системы повторяет свойства критической точки при n=2. Её ордината равна разнице двух первых приращений ординат (или сумме ординат двух первых направляющих точек за вычетом единицы), а абсцисса – сумме приращений их абсцисс. Как и критическая точка при n=2, самая нижняя точка всегда лежит на прямой линии 2-й системы между 1-й и 3-й направляющими точками; при УК₂=1 самая нижняя точка совпадает с 3-й направляющей точкой (рис.4-1, n=3, n=5, n=7).

Несмотря на внешнее сходство, самая нижняя точка при n?2 по ряду очевидных причин не может лежать на кривой.

Во-первых, её ордината меньше ординаты критической точки, которая находится под кривой и никогда – над кривой (рис.4-3-1).

Во-вторых, ближайшие к кривой точки (включая гипотетические точки на кривой) на прямых линиях 1-й системы самыми нижними быть не могут (прил.3-1-2 и 3-1-3).

В-третьих, ордината самой нижней точки меньше вертикальной проекции даже одного первого звена ломаной линии – кривой (2-1) – рис.4-3-2. Тем более, она меньше суммы той же проекции первого звена со следующими проекциями, как минимум – при n=3 – четырёх звеньев.

Рис.4-3-1. Ординаты критической точки, кривой (2-1) и самой нижней точки на второй прямой 1-й системы параллельных линий, соединяющих точки; легенда на обоих графиках.

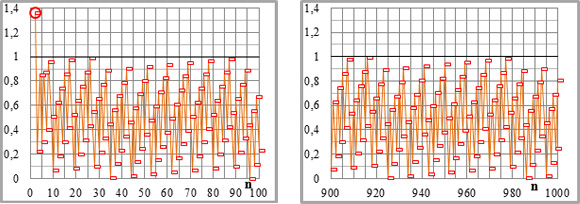
Рис.4-3-2. Соотношение ординаты самой нижней точки на второй прямой 1-й системы параллельных линий (О_НЖН) с вертикальной проекцией первого звена ломаной линии, условно именуемой кривой (2-1). Красный кружок при n=2 – единственное значение соотношения больше единицы (0,24264 / 0,17815=1,36204).

Приложение 4-4

Варианты расчёта координат точек при n=2

Таблица 4-4-1

Модель расчёта координат точек на кривой и над ней при n=2

Содержание граф табл.4-4-1 с номерами:

1. №№ п/п – i.

2. Абсциссы направляющих точек – приращения абсцисс.

5. Расчёт ординат направляющих точек – приращений ординат.

i	Абсциссы точек			Ординаты точек
	хНПР	Точки на кривой	Точки над кривой	х*М–целое число {М=[(v2)–1]}	Точки на кривой	Точки над кривой
1	2	3	4	5	6	7
0	0	0		0	0
1	1		0+1=1	1*М–0=		0,414214
2	2	0+1+2=3		3*М–1=	0,2426407
3	5		3+5=8	8*М–3=		0,313708
4	12	3+5+12=20		20*М–8=	0,2842713
5	29		20+29=49	49*М–20=		0,296465
6	70	20+29+70=119		119*М–49=	0,2914139
7	169		119+169=288	288*М–119=		0,293506
8	408	119+169+408=696		696*М–288=	0,2926394
9	985		696+985=1681	1681*М–696=		0,292998
10	2378	696+985+2378=4059		4059*М–1681=	0,2928497
11	5741		4059+5741=9800	9800*М–4059=		0,292911
12	13860	9800+13860=23660		23660*М–9800=	0,2928857

Таблица 4-4-2

Модель расчёта ординат точек на кривой и над ней при n=2

i	Ординаты точек
	Расчёт через М=[(v2)–1]	Точки на кривой	Точки над кривой
1	5	6	7
0		0
1	М1=[(v2)–1]=0,4142135624		0+М1=0,414213562
2	М2=2М1–М0= –0,171572875	0,414213562–М2=0,24264068
3	М3=М1–2М2=0,071067812		0,242640687+М3=0,31370850
4	М4=2М3–М2= –0,029437252	0,313708499–М4=0,28427125
5	М5=М3–2М4=0,012193309		0,284271247+М5=0,29646456
6	М6=2М5–М4= –0,0050506339	0,296464556–М6=0,29141392
7	М7=М5–2М6=0,00209204105		0,291413922+М7=0,29350596
8	М8=2М7–М6= –8,66551777e-4	0,293505963–М8=0,29263941
9	М9=М7–2М8=3,589374986e-4		0,292639412+М9=0,29299835
10	М10=2М9–М8= –1,4867678e-4	0,292998349–М10=0,2928497
11	М11=М9–2М10=6,15839387e-5		0,292849672+М11=0,2929113
12	М12=2М11–М10= –2,5508903e-5	0,292911256–М12=0,2928857

Таблица 4-4-3

Модель расчёта абсцисс точек на кривой и у горизонтальных ограничений графика при n=2 (все УК_i=2)

№№	Абсциссы направляющих точек
	У нижнего ограничения графика хНПР-i+2=хНПР-i+хНПР-i+1*УКi	На кривой (межсистемных точек) b2–a2 / 2*a*b	У верхнего ограничения графика (см. графу 2)
1	2	3	4
0			0
1	1
2		b2–a2=22–12=3	0+1*2=2
2		(2*a*b =2*1*2=4)1)
3	1+2*2=5
3	a2+b2=12+22=5
3	v[32+(3+1)2]=5
4		(52–22=21)1)	2+5*2=12
4		2*2*5=20
5	5+12*2=29
5	a2+b2=22+52=29
5	v[202+(20+1)2]=29
6		122–52=119	12+29*2=70
6		(2*5*12=120)
7	29+70*2=169
7	52+122=169
7	v[1192+(119+1)2]=169
8		(292–122=697)	70+169*2=408
8		2*12*29=696
9	169+408*2=985
9	122+292=985
9	v[6962+(696+1)2]=985
10		702–292=4059	408+985*2=2378
10		(2*29*70=4060)
11	985+2378*2=5741
11	292+702=5741
11	v[40592+(4059+1)2]=5741
12		(1692–702=23661)	2378+5741*2=13860
12		2*70*169=23660
13	5741+13860*2=33461
13	702+1692=33461
13	v[236602+(23660+1)2]=33461
14		4082–1692=137903	13860+33461*2=80782
14		(2*169*408=137904)
15	33461+80782*2=195025
15	1692+4082=195025
15	v[1379032+(137903+1)2]=195025
и т.д.

¹⁾ В скобках – второе число пифагоровой тройки, равное её первому числу плюс единица.

Приложение 4-5

Суммарные приращения ординат точек и прирост ординаты кривой в ЗНН при n=2

Интервал абсцисс	Приращения ординат точек		Прирост ординаты кривой1)
	в интервале	нарастающим итогом	в интервале	нарастающим итогом
1	2	3	4	5
Первый вариант
0-1	0,414213	0,414214	0,178146		0,178146
1-2	0,414213	0,828427	0,044730		0,222876
2-3	0,414213	1,242641–1=0,242641	0,019765		0,242641
Второй вариант
0-1	0,414213	0,414214	0,178146		0,178146
1-2	–0,085786	0,328427	0,044730		0,222876
2-3	–0,085786	0,242641	0,019765		0,242641

¹⁾ Прирост ординаты кривой по вариантам не меняется.

Суммарные приращения ординат точек (с буквенными обозначениями) и прирост ординаты кривой в ЗНН при n=2

Интервал абсцисс	Приращения ординат точек		Прирост ординаты кривой1)
	в интервале	нарастающим итогом	в интервале	нарастающим итогом
1	2	3	4	5
Первый вариант
0-1	ПО/1	ПО/1=0,414214	0,178146		0,178146
1-2	ПО/1	2*ПО/1=0,828427	0,044730		0,222876
2-3	ПО/1	3*ПО/1–1=0,242641	0,019765		0,242641
Второй вариант
0-1	ПО/1	ПО/1=0,414214	0,178146		0,178146
1-2	–ПО/2/2	ПО/1–ПО/2/2=0,328427	0,044730		0,222876
2-3	–ПО/2/2	ПО/1–ПО/2=0,242641	0,019765		0,242641

¹⁾ Прирост ординаты кривой по вариантам не меняется.

Приращения ординат точек. Ординаты кривой (О_КРВ) и её прирост (О_{КРВ x=i+1}–О_{КРВ x=i})

Ординаты кривой и её приросты	Натуральные числа	Приращения ординат точек			Радикалы			Сумма1)
		ПО/1	ПО/2	ПО/3
1	2	3	4	5	6	7	8	9=?28
ОКРВ x=2	4		–ПО/2			–(v13)		=0,222876
–ОКРВ x=1	2	+ПО/1			–(v5)			=0,178146
ОКРВx=2–ОКРВx=1	2	–(ПО/1+ПО/2)			+(v5)	–(v13)		=0,044730
ОКРВ x=3	5		ПО/2+ПО/3				–(v25)	=0,242641
–ОКРВ x=2	4		–ПО/2			–(v13)		=0,222876
ОКРВx=3–ОКРВx=2	1	+ПО/1				+(v13)	–(v25)	=0,019765

¹⁾ Сумма граф 2–8.

Приложение 4-6

Обоснование принадлежности кривых к типу эллиптических

Для обоснования принадлежности кривых к типу эллиптических, или более определённо – их возможности воспроизводить себе подобные точки – формализуется связь абсциссы точки касания (x_КСТ) и новообразованной абсциссы (X) точки пересечения двух линий: а) кривой (2-1) и б) хорды (4-6-1), исходящей из начала координат и параллельной касательной – нулевой хорды. Заменяя громоздкое вычитаемое в (2-12) символом T, получаем уравнение нулевой хорды:

О_У=Х* tg?_КСТ = Х*[(ⁿv2)–T], (4-6-1)

где О_У – ордината точки пересечения кривой (2-1) – хордой.

Параметр T рассчитывается в точке касания. Для определения новообразованной абсциссы точки пересечения (Х) совместно решаются уравнения (2-1) и (4-6-1):

C+Х*(ⁿv2)–ⁿv[Хⁿ+(Х+C)ⁿ] = Х*[(ⁿv2)–T]

C+Х*(ⁿv2)–ⁿv[Хⁿ+(Х+C)ⁿ] = Х*(ⁿv2)–TХ

C+TХ = ⁿv[Хⁿ+(Х+C)ⁿ]

(C+TХ)ⁿ = Хⁿ+(Х+C)ⁿ (4-6-2)

Независимо от показателя степени n, последующие преобразования (4-6-2) приводят к уравнению (4-6-3) с биномиальными коэффициентами:

Xⁿ(2–Tⁿ)+nСX^n–1(1–T^n–1)+… …+С^kX^n–k{[n(n–1)…(n–k+1)]/1*2*…*k}(1–T^n–k)+… …+nС^n–1X(1–T)=0 (4-6-3)

Если T рационально, а это может быть только тогда, когда точка касания лежит на кривой, и её абсцисса обеспечивает целочисленное решение радикала ⁿv[x_КСТⁿ+(х_КСТ+1)ⁿ], в (4-6-3) все коэффициенты при Х – тоже рациональные числа. В этом случае один из корней – абсцисса точки пересечения – может быть целым, рациональным, но и иррациональным числом. Если же Т – иррационально, рациональным остаётся только коэффициент первого члена, а все остальные коэффициенты и корни (4-6-3) – иррациональны. Таким образом, посредством параметра T – через систему двух параллельных линий – касательной и нулевой хорды – информация о характере точки касания передаётся в точку пересечения. Подобный механизм воспроизводства характерных точек может свидетельствовать о принадлежности кривых (2-1) к типу эллиптических.

Приведенное обоснование далеко от классического – с использованием дискриминанта, – но кривые (2-1) ещё дальше от эллиптических кривых, заданных в канонической форме, то есть уравнениями с целочисленными коэффициентами и неизвестными во второй и третьей степени.

Основу механизма воспроизводства характерных точек составляют два прямоугольных треугольника, выделенные на графиках рис.4-6-1 жирными линиями. Катеты треугольников параллельны осям графика, гипотенузы параллельны по условиям построения. Соответственно, все углы треугольников равны, сами треугольники подобны, а их стороны пропорциональны. Запуск механизма воспроизводства возможен при совпадении с кривой хотя бы одной ненулевой целочисленной точки – первой точки. Лишь в этой точке параметр Т в формуле углового коэффициента касательной (2-12) приобретает рациональное значение, и один из корней (4-6-3) – абсцисса точки пересечения кривой и нулевой хорды – может быть целым числом.

При n>2 критическая точка не лежит на кривой, соответственно, – угловые коэффициенты касательных к кривой при х_КР=х_КСТ и прямых линий, соединяющих точки, не совпадают, то есть гипотенузы треугольников, составляющих основу механизма воспроизводства, не параллельны, треугольники не подобны. Оставаясь эллиптическими, кривые не могут воспроизводить целочисленные точки из-за отсутствия на кривой первой точки (или второй – с учётом начала координат). Её отсутствие при n>2 обосновано в разделе 4.

Применительно к абсциссам (Х) точек пересечения нулевой хорды и кривой, пифагоровы тройки – лишь частный случай более общей закономерности.

Если n=2, уравнение (4-6-3) упрощается до

Х²*(2–Т²)+2С*X*(1–Т)=0, (4-6-4)

и после сокращения на Х [один из корней (4-6-3) и (4-6-4) соответствует началу координат] – до

Х*(2–Т²)+2C*(1–Т)=0, откуда

Х*(2–Т²)=2C*(Т–1) и

Х=2C*(Т–1)/(2–Т²) (4-6-5)

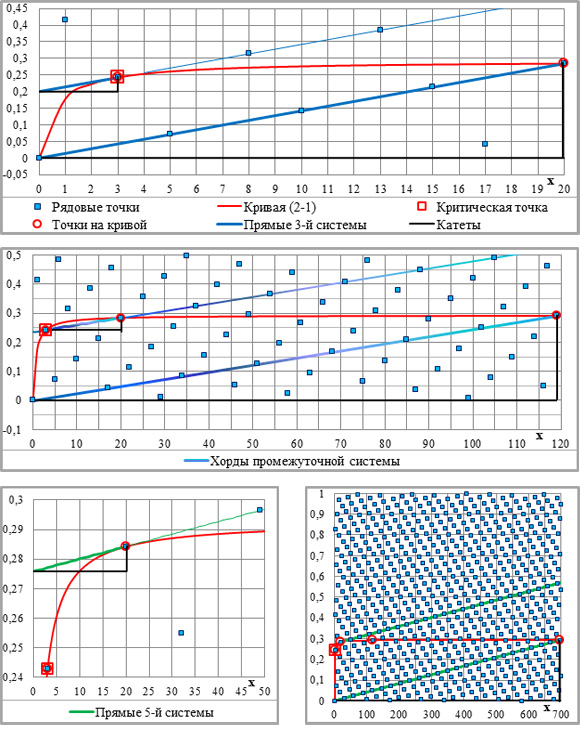
Рис.4-6-1. Кривая (2-1) и подобные треугольники; n=2, С=1, целочисленные точки на кривой – х=3, х=20, х=119, х=696 (легенда – последовательно на всех графиках).

Верхний график – П_А/3=5, П_О/3=[(v2)–1]³=0,071068, tg?_3-й=[(v2)*5–7]/5=(v2)–7/5=0,014214.

Второй график сверху. В единой системе угловых коэффициентов прямых линий, соединяющих точки, определённое значение имеют межсистемные прямые, в частности, хорды, соединяющие точки, лежащие на кривой. В данном конкретном случае рядовые приращения координат для хорды (П_А/х и П_О/х) составляют: П_А/(3-4)=П_А/3+П_А/4=5+12=17 и П_О/(3-4)=П_О/3–П_О/4=0,04163, tg?_3-4-й=[(v2)*17–24]/17=(v2)–24/17=0,002449.

Нижние графики – П_А/5 = 29, П_О/5=[(v2)–1]⁵=0,01219, tg?_5-й=[(v2)*29–41]/29=

=(v2)–41/29=4,2046e-4.

Продекларированная выше закономерность для пифагоровых троек состоит в том, что для любой целочисленной абсциссы точки касания x_КСТ справедливо равенство:

Х+v[Х²+(Х+С)²] = (2x_КСТ+С)²/С, (4-6-6)

то есть сумма в его левой части является рациональным или целым числом, а произведение

{Х+v[Х²+(Х+С)²]}*C = (2x_КСТ+С)² (4-6-7)

– целым числом, несмотря на то, что и параметр Т, и Х, и v[Х²+(Х+С)²] – преимущественно иррациональные числа, кроме случаев с собственно пифагоровыми тройками (табл.4-6-1).

Таблица 4-6-1

Параметры с новообразованной абсциссой точки пересечения (Х) кривой (2-1) и хорды (4-6-1) y=Х*tg ?_КСТ

Показатели	Численное значение показателей
х	3	4	5	5	300
С	7	7	7	2	2
x+С	10	11	12	7	302
х+(x+С)=2x+С	13	15	17	12	602
x2+(x+С)2	109	137	169	74	181204
v[х2+(х+С)2]	10,44030651	11,70469991	13	8,602325267	425,6806315
T=(2х+С)]/v[х2+(х+С)2]	1,245174171	1,281536487	1,307692308	1,394971665	1,414205758
Х=2С*(Т-1)/(2–Т2)	7,635424176	11,02014248	14,85714286	29,22790321	75055,74014
Х+С	14,63542418	18,02014248	21,85714286	31,22790321	75057,74014
Х2+(Х+С)2	272,4953432	446,1690750	698,4693878	1829,452264	11267028483
v[Х2+(Х+С)2]	16,50743297	21,12271469	26,42857143	42,77209680	106146,2599
Х+v[Х2+(Х+С)2]	24,14285714	32,14285714	41,28571429	72	181202
{Х+v[Х2+(Х+С)2]}*C=(2x+С)2	169	225	289	144	362404
Показатели	Численное значение показателей
х	11	12	13	14	15
С	1	1	1	5	5
x+С	12	13	14	19	20
х+(x+С)=2x+С	23	25	27	33	35
x2+(x+С)2	265	313	365	557	625
v[х2+(х+С)2]	16,27882060	17,69180601	19,10497317	23,60084744	25
T=(2х+С)]/v[х2+(х+С)2]	1,412878769	1,413083547	1,413244591	1,398254875	1,4
Х=2С*(Т-1)/(2–Т2)	218,8257474	258,5903006	301,6685514	88,73118624	100
Х+С	219,8257474	259,5903006	302,6685514	93,73118624	105
Х2+(Х+С)2	96208,06696	134256,0678	182612,1669	16658,75869	21025
v[Х2+(Х+С)2]	310,1742526	366,4096994	427,3314486	129,0688138	145
Х+v[Х2+(Х+С)2]	529	625	729	217,8	245
{Х+v[Х2+(Х+С)2]}*C=(2x+С)2	529	625	729	1089	1225

Приложение 4-7

Схемы общего доказательства теоремы Ферма

Обе приведенные ниже схемы рассматриваются лишь как дополнение к основному доказательству (объяснению) несовместимости точек и кривой в разделе 4 – для освещения возможностей, связанных с эллиптическими кривыми, и графической схемы в целом.

Схема общего доказательства теоремы выглядит следующим образом. Предполагается, что какая-то гипотетическая рядовая точка лежит на кривой. Через неё проводится касательная, а из начала координат, параллельно ей, – хорда (нулевая хорда); на пересечении хорды с кривой – благодаря свойству (способности) эллиптических кривых воспроизводить себе подобные точки – должна лежать целочисленная точка. Если в найденной точке повторить подобную операцию, а затем повторить её ещё бесконечное множество раз, очередная целочисленная точка ложится на кривую там, где она «достигает» своего предела. Но, как было показано в разделе 3, ни одна точка при n>2 несовместима с пределом кривой. Следовательно, первоначальное предположение о существовании гипотетической точки, лежащей на кривой, неверно, и теорема доказана.

Схема доказательства теоремы с использованием в качестве опорной базы критической точки отличается от схемы, изложенной выше, лишь по форме. Меняется порядок проведения линий: сначала нулевая хорда – от гипотетической точки, лежащей на кривой, к началу координат, затем параллельная ей касательная, далее – снова нулевая хорда и параллельная ей касательная и т.д. При подобной итерации воображаемая целочисленная точка касания смещается не вправо – к пределу кривой, а влево – к ЗНН, и, в конце концов, должна совпасть с ограничивающей её критической точкой. Но, как показано в разделе 4, критическая точка при n>2 несовместима с кривой. Следовательно, первоначальное предположение о существовании лежащей на ней гипотетической точки неверно, и теорема доказана.

Определённостью своего положения критическая точка выгодно отличается от предела кривой. Тем не менее, её использование в качестве опорной базы доказательства теоремы методом «от противного» предполагает необходимость дополнительного обоснования. Дело в том, что даже при n=2 и С>1 критические точки не всегда лежат на кривой (рис.4-7-1, 4-7-2, 4-7-3). Более того, при тех же n=2 и С>1 не все точки, лежащие на эллиптической кривой, способны к воспроизводству с помощью касательных и параллельных им нулевых хорд.

В формулировке теоремы Ферма вторая степень исключается из рассмотрения специальной оговоркой. Но кривая (2-1) при n=2 – единственный объект, позволяющий предметно исследовать описанный выше процесс итерации и реальные величины, с которыми проводятся повторяющиеся математические операции, – абсциссы целочисленных точек, угловые коэффициенты касательных и параллельных хорд. Именно поэтому в работе рассматриваются пифагоровы тройки, все первые числа которых соответствуют абсциссам точек, лежащих на кривой.

Используя в качестве классификационного признака параметр С, среди бесконечного множества пифагоровых троек можно выделить три подмножества: первородных, побочных (парных) и производных троек.

У первородных троек параметр С равен единице, у побочных (парных) – некоторым простым числам и их степеням, у производных – произведению величины С двух предыдущих типов троек на любое натуральное целое число (на М_Н – множитель). Самостоятельным типом производные тройки не являются, сохраняя большинство свойств множимых троек, в частности, их разную способность к воспроизводству. Два первых типа троек можно находить по стандартным формулам – 2ab, a²–b² и a²+b², – где a и b – целые числа. Для поиска производных троек эти формулы также применимы, но числа a и b обычно имеют в этом случае иррациональное значение (если множитель М_Н не является квадратом какого-либо числа).

Лишь первородные тройки обладают способностью к расширенному воспроизводству (табл.4-7-1, 4-7-2). Достаточно просто решается вопрос о происхождении первой точки первой тройки с абсциссой x=3 (праматери всех пифагоровых троек). Её воспроизводство с помощью нулевой хорды (0-3*С) и параллельной ей касательной предполагает наличие в ЗНН целочисленной точки касания, что невозможно по определению. Однако абсцисса точки касания (х_КСТ) приобретает в этом случае не целочисленное, но характерное значение: х_КСТ={[(v2)–1]+0,5}*C=[(v2)–0,5]*C=0,91421*С; не менее характерна и ордината точки касания: [(v2)–1]²*С=0,17157*С (рис.4-7-2).

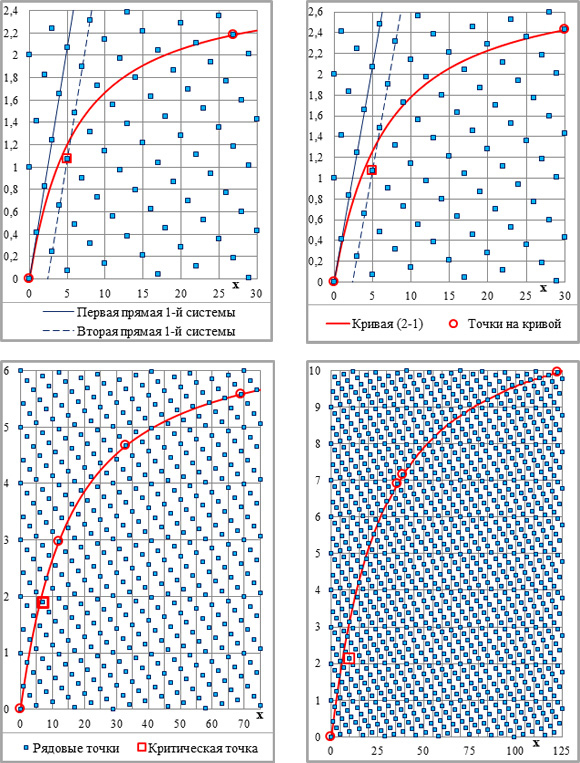
Рис.4-7-1. Положение критической точки вне кривой (2-1) – при наличии других точек, лежащих на ней (легенда – на трёх первых графиках); n=2.

Верхняя пара графиков – слева – С=9, точка на кривой – х=27,

справа – С=10, точка на кривой – х=30;

нижняя пара графиков – слева – С=23, точки на кривой – х=12, х=33 и х=69,

справа – С=41, точки на кривой – х=36, х=39 и х=123

Таблица 4-7-1

Воспроизводство первых чисел первородных пифагоровых троек с помощью параметра Т касательной к кривой (2-1) и параллельной нулевой хорды

№№ п/п (i)	Абсцисса точки касания: х	Параметрыглавной – единой и неизменной системы касательных и хорд		Х=2С*(T–1) / (2–T2) (№№ п/п в графе 1)
		T=(2х+1)/v[х2+(х+1)2]	tg?=(v2)–T
1	2	3	4	5
0	0	1	0,41421356237310	–1)
б/н	0,5+[(v2)–1]	1,3333333333333	0,08088022903976	3 (1)
1	3	1,4	0,01421356237310	20 (2)
2	20	1,413793103448276	4,204589248192e-4	696 (4)
3	119	1,414201183431953	1,237894114239e-5	23660 (6)
4	696	1,414213197969543	3,644035519016e-7	803760 (8)
5	4059	1,414213551646055	1,072704035450e-8	27304196 (10)
6	23660	1,414213562057321	3,15774586174e-10	927538920 (12)
7	137903	1,414213562363800	9,29553591873e-12	31509019100 (14)
8	803760	1,414213562372821	2,7363502888e-13	1070379110496 (16)
9	4684659	1,414213562373087	8,05506317061e-15	36361380737780 (18)
10	27304196	1,414213562373095	2,37118920586e-16	1235216565974040 (20)

¹⁾ Нет пересечения кривой и нулевой хорды [см. в тексте неравенство (3-1)]

Таблица 4-7-2

Воспроизводство первых чисел первородных пифагоровых троек с помощью параметра Т хорды, дважды секущей кривую, и параллельной нулевой хорды

(№№ п/п в графе 1 табл.4-7-1)	Абсциссы точек пересечения		Параметрыглавной системы угловых коэффициентов		Х=2С*(T–1) / (2–T2) (№№ п/п в графе 1 табл.4-7-1)
	хi	xj	Т=(v2)–(РО/РА)1)	tg?=(v2)–T
1	2	3	4	5	6
0-1	0	3	1,333333333	0,08088022904	3 (1)
1-2	3	20	1,411764706	0,002448856491	119 (3)
2-3	20	119	1,414141414	7,214823168e-5	4059 (5)
3-4	119	696	1,414211439	2,123898225e-6	137903 (7)
4-5	696	4059	1,414213500	6,252177183e-8	4684659 (9)
5-6	4059	23660	1,414213561	1,840469162e-9	159140519 (11)
6-7	23660	137903	1,414213562	5,41783537e-11	5406093003 (13)
7-8	137903	803760	1,414213562	1,59486182e-12	183648021599 (15)
8-9	803760	4684659	1,414213562	4,69483487e-14	6238626641379 (17)
9-10	4684659	27304196	1,414213562	1,38203035e-15	211929657785303 (19)
10-11	27304196	159140519	1,414213562	4,06831750e-17	7199369738058939 (21)
1-3	3	119	1,413793103	4,204589248e-4	696 (4)
1-4	3	696	1,414141414	7,214823168e-5	4059 (5)
1-5	3	4059	1,414201183	1,237894114e-5	23660 (6)
1-6	3	23660	1,414211439	2,123898225e-6	137903 (7)
1-7	3	137903	1,414213198	3,644035519e-7	803760 (8)
1-8	3	803760	1,414213500	6,252177183e-8	4684659 (9)
3-7	119	137903	1,414213552	1,072704035e-8	27304196 (10)
3-8	119	803760	1,414213561	1,840469162e-9	159140519 (11)

¹⁾ Разность ординат Р_О={1+х_i+1*(v2)–v[х_i+1²+(х_i+1+1)²]}–{1+х_i*(v2)–v[х_i²+(х_i+1)²]}

Разность абсцисс (Р_А) точек пересечения: Р_А=х_i+1–х_i

Другой способ: tg?=[(v2)*(х_i+1–х_i)–целое число] / (х_i+1–х_i); Т=(v2)–tg?.

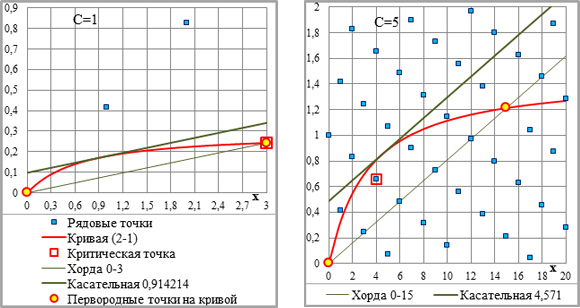
Рис.4-7-2. Воспроизводство точек в ЗНН. Левый график – С=1, правый – С=5. Легенда – на обоих графиках; цифры при касательных и хордах – абсциссы точек пересечения и касания [кроме обозначения кривой – (2-1)]; 0,914214=0,5+[(v2)–1], 4,5711=5*{0,5+[(v2)–1]}

Первородным тройкам принадлежит монопольное право формировать главную – единую и неизменную систему угловых коэффициентов касательных и хорд (табл.4-7-1, 4-7-2).

Напомним, что независимо от показателя степени, только в пределах элементарного графика (при С=1) формируются угловые коэффициенты параллельных линий, соединяющих точки, и соответствующие им приращения ординат и абсцисс – рядовые и укрупнённые (табл.2-1).

Побочные тройки образуются только парами, поскольку каждая хорда два раза пересекает кривую, откуда их второе название. Две точки пересечения естественно находятся по бокам от точки касания, откуда их первое название. Все параметры побочных (парных) троек, включая их первые числа, равные абсциссам точек, лежащих на кривой, длину горизонтальной проекции хорд между этими точками и угловые коэффициенты хорд, предопределены параметрами первородных троек.

Компьютерная программа Microsoft Excel предоставляет широкие возможности для поиска параметров С, обеспечивающих генерацию побочных (парных) троек. Другим способом служит совместное решение уравнений двух линий – кривой (2-1) и секущей её хорды:

С+х*(v2)–v[x²+(x+C)²] = В_ХРД+х*tg? = В_ХРД+х*[(v2)–T], (4-7-1)

где tg? и Т – параметры главной – единой и неизменной системы угловых коэффициентов касательных и хорд (табл.4-7-1, графы 3, 4 и табл.4-7-2, графы 4, 5),

В_ХРД – ордината точки пересечения хордой вертикальной линии, исходящей из начала координат, причём В_ХРД=К_КРТН*О_КРТН,

где К_КРТН – коэффициент кратности (числа натурального ряда) и

О_КРТН – основание (объект) кратности; О_КРТН=1/v[x_i²+(x_i+C)²] – для касательных единой и неизменной системы угловых коэффициентов и О_КРТН=1/(x_i+1–x_i) – для хорд той же системы,

где x_i и x_i+1 – абсциссы первых точек первородных троек (i – порядковый номер первого числа пифагоровой тройки в первой графе табл.4-7-1: i=0 – х=0, i=1 – x=3, i=2 – x=20 и т.д.).

Преобразования равенства (4-7-1), включая подстановку В_ХРД=К_КРТН*О_КРТН, позволяют получить квадратное уравнение (4-7-2), два корня которого (х) являются абсциссами точек пересечения кривой (2-1) и хорды y=В_ХРД+х*tg?:

(2–Т²)х²–2*[С*(Т–1)–К_КРТН*Т*О_КРТН]х+[2С*К_КРТН*О_КРТН–(К_КРТН)²*(О_КРТН)²]=0 (4-7-2)

Уравнение (4-7-2) включает три неизвестных – х, С, К_КРТН – и может решаться только перебором вариантов С и К_КРТН (см. рис.4-7-3, 4-7-4 и табл. к ним).

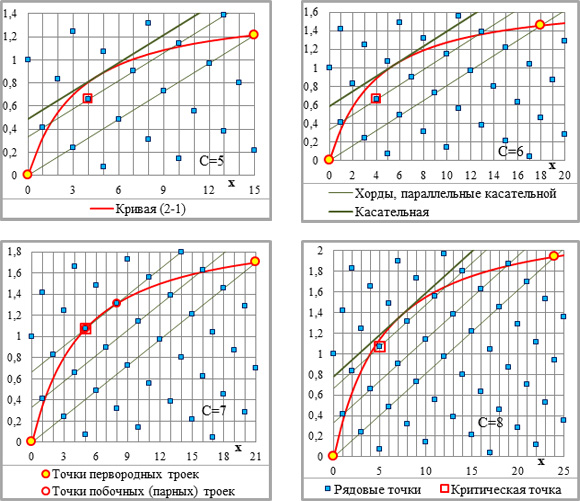
Рис.4-7-3. Воспроизводство побочных (парных) троек на кривой (2-1) в интервале 0–3*С при n=2. Легенда на всех графиках.

Таблица к рис.4-7-3

Принятые значения: i=0; x_i–x_i+1=0–3; tg?_КСТ=tg?_ХРД=[3*(v2)–4]/3=(v2)–4/3=0,08088;

Т=(v2)–tg?=1,3333, О_КРТН=1/3=0,33333

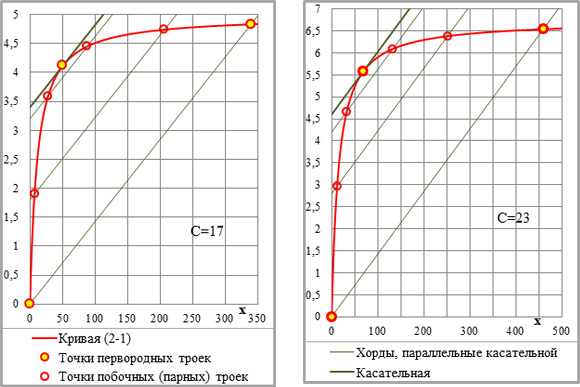
Рис.4-7-4. Воспроизводство побочных (парных) троек на кривой (2-1) в интервале 0–3*С–20*С при n=2. Легенда на обоих графиках. Ниже жирным шрифтом выделены первые числа первородных пифагоровых троек, обычным – первые числа побочных (парных) троек.

Левый верхний график – С=17, х=0-7-28-51-88-207-340.

Правый верхний график – С=23, х=0-12-33-69-133-252-460.

Таблица к рис.4-7-4

Принятые значения: i=1, x_i=3, tg?_КСТ=tg?_ХРД=[5*(v2)–7]/5=(v2)–7/5=0,01421356; Т=(v2)–tg?_КСТ=1,4, О_КРТН=1/5=0,2

¹⁾ Абсцисса точки касания

Побочные (парные) тройки и тройки, производные от них, не способны к воспроизводству. Если с этой целью используются касательная к кривой с абсциссой точки касания, равной первому числу побочной (парной) тройки, и параллельная касательной нулевая хорда, то новообразованная абсцисса (Х) становится не целым, но рациональным числом (рис.4-7-5). Если для воспроизводства используется хорда между двумя точками побочных (парных), возможны различные варианты, но большинство новообразованных абсцисс – те же рациональные числа.

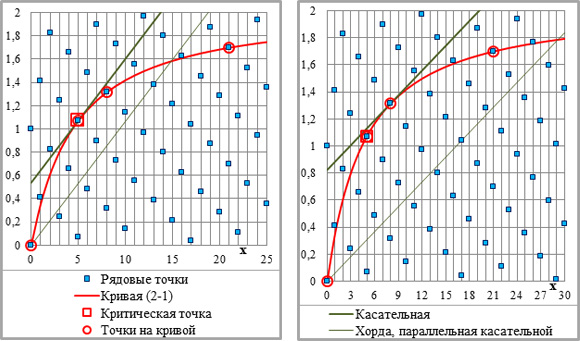
Рис.4-7-5. Воспроизводство первых чисел пифагоровых троек с помощью параметра Т касательной к кривой с абсциссами точек касания, соответствующими первым числам побочных (парных) троек; С=7. Линии, параллельные касательным, воспроизводят на кривой точки с рациональными абсциссами: х=14,86*7=104 и х=29,14*7=204.

Первородные тройки непосредственно или косвенно – через параметры побочных (парных) троек – определяют и параметры производных троек. Отсюда следует главный вывод изучения пифагоровых троек: процесс итерации, необходимый для общего доказательства теоремы с использованием способности эллиптических кривых воспроизводить себе подобные точки, может и должен проводиться в пределах элементарного графика, то есть при С=1. В этом случае критическая точка (с абсциссой х_КР=3) лежит на кривой и так же, как и все другие целочисленные точки на ней, способна к воспроизводству. Другими словами, доказательство теоремы при параметре С, равном единице, можно распространить на все его значения.

С учётом сделанного вывода следует соответственно изменить вводную фразу предложенных в начале настоящего раздела схем общего доказательства теоремы, добавив подчёркнутый ниже фрагмент: «Предполагается, что в пределах элементарного графика, то есть при C=1, какая-то гипотетическая рядовая точка лежит на кривой…» (и далее по тексту).

Уместно ещё раз напомнить, что при любом показателе степени основные параметры всех графических схем – приращения абсцисс, ординат и угловые коэффициенты прямых линий, соединяющих точки, – формируются на элементарном графике (первые абзацы раздела 2).

И.И. Лещенко